गणितातील मूलभूत आणि महत्त्वपूर्ण संकल्पनांपैकी एक म्हणजे पूर्ण संख्या. आपण दररोज व्यवहारात ज्या संख्यांचा उपयोग करतो, त्या पैकी बऱ्याचशा संख्यांचा समावेश पूर्ण संख्यांमध्ये होतो.
या लेखात आपण जाणून घेणार आहोत:
- पूर्ण संख्या म्हणजे काय?
- त्याचे मुख्य गुणधर्म (Properties) कोणते?
- इतर संख्यांपासून पूर्ण संख्या कशा वेगळ्या आहेत?
- आणि अभ्यासासाठी उपयोगी उदाहरणे व सराव प्रश्न.
जर तुम्ही इयत्ता 6वी ते 8वी चा अभ्यास करत असाल, किंवा पालक, शिक्षक किंवा स्पर्धा परीक्षेचा अभ्यास करणारे असाल – तर हाच लेख तुम्हाला पूर्ण संख्यांचा अभ्यास करण्यासाठी मार्गदर्शक ठरेल.
चला तर मग सुरुवात करूया संख्यांच्या या शुद्ध आणि सोप्या जगात — पूर्ण संख्यांच्या समजुतीने!
पूर्ण संख्यांची व्याख्या (Definition of Whole Numbers in Marathi):
पूर्ण संख्या म्हणजे अशा संख्यांचा समूह ज्यामध्ये शून्य (0) पासून सुरू होणाऱ्या सर्व नैसर्गिक संख्यांचा (1, 2, 3, 4, …) समावेश होतो. या संख्यांमध्ये कोणतीही दशांश, भिन्न किंवा ऋण (negative) संख्या नसते.
पूर्ण संख्यांचा संच (W):
- पूर्ण संख्या दर्शवण्यासाठी W हे चिन्ह वापरले जाते.
W = {0, 1, 2, 3, 4, 5, 6, ...}- यामध्ये:
- शून्य (0) हा समाविष्ट आहे
- सर्व नैसर्गिक संख्या (1, 2, 3, …) समाविष्ट आहेत
- ऋण संख्या, भिन्न संख्या आणि दशांश संख्या यांचा समावेश नाही
- सर्व पूर्ण संख्यांना पूर्णांक (Integers) म्हणता येत नाही कारण पूर्णांकांमध्ये ऋण संख्या (Negative Numbers) पण असतात.
- पूर्ण संख्यांमध्ये फक्त धन पूर्णांक (Positive Integers) आणि 0 असतो.
- उदाहरणे:
- 0, 4, 17, 100 – पूर्ण संख्यांचे उदाहरण
- -5, 3.5, ½ – पूर्ण संख्यांचे उदाहरण नाहीत
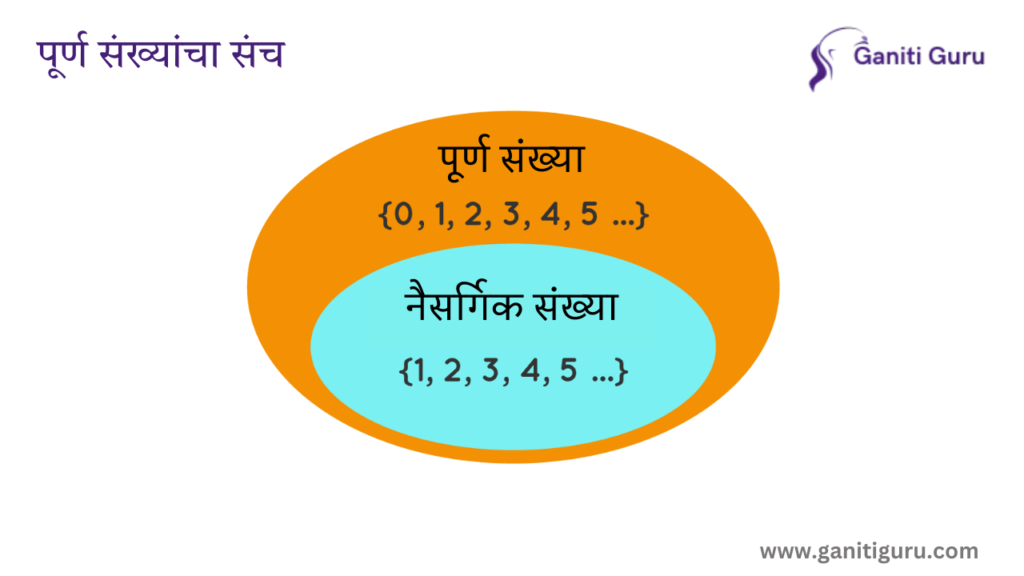
लक्षात ठेवा:
सर्व नैसर्गिक संख्या या पूर्ण संख्यांमध्ये येतात, पण सर्व पूर्ण संख्या नैसर्गिक नसतात.
पूर्ण संख्यांचे गुणधर्म (Properties of Whole Numbers in Marathi):-
1. Closure Property in Marathi :-
जेव्हा दोन पूर्ण संख्यांची बेरीज किंवा गुणाकार केले जाते, तेव्हा त्याचा मिळणारे उत्तर देखील पूर्ण संख्या असतो.
जर a आणि b या दोन्ही पूर्ण संख्या असतील, तर:
1) बेरीजसाठी गुणधर्म (Addition):
- a + b = c, जिथे c हीसुद्धा पूर्ण संख्या असेल
- उदाहरण:
- 8+3=11 → 11 ही देखील पूर्ण संख्या आहे.
2) गुणाकारासाठी गुणधर्म (Multiplication):
- a × b = c, जिथे c हीसुद्धा पूर्ण संख्या असेल
- उदाहरण:
- 4×5=20 → 20 हीही पूर्ण संख्या आहे.
3) वजाबाकीसाठी गुणधर्म (Subtraction):
- हा गुणधर्म वजाबाकीला लागू होत नाही.
- उदाहरण:
- 3−7=−4 → -4 ही पूर्ण संख्या नाही (ती पूर्णांक आहे, पण पूर्ण संख्या नाही).
2. Commutative Property in Marathi :-
जर दोन पूर्ण संख्यांची बेरीज किंवा गुणाकार करताना त्यांचा क्रम बदलला, तरी उत्तर तेच येते.
1) बेरीजसाठी गुणधर्म (Addition):
- जर a आणि b या दोन पूर्ण संख्या असतील, तर:
- a + b = b + a
- उदाहरण:
- 5+7=12
- 7+5=12
- म्हणजेच, 5+7=7+5
2) गुणाकारासाठी गुणधर्म (Multiplication):
- जर a आणि b या दोन पूर्ण संख्या असतील, तर:
- a × b = b × a
- उदाहरण:
- 4×6=24
- 6×4=24
- म्हणजेच, 4×6=6×4
3) वजाबाकी आणि भागाकर यांना हा गुणधर्म लागू होत नाही.
- उदाहरण:
- 8−3=5, पण 3−8=−5(जो पूर्ण संख्या नाही)
- म्हणून वजाबाकीला हा गुणधर्म लागू नाही.
3. Associative Property in Marathi :-
तीन नैसर्गिक संख्यांची बेरीज किंवा गुणाकार करताना, संख्यांचा समूह बदलला तरीही अंतिम उत्तर सारखं राहतो.
जर a, b, c या सर्व पूर्ण संख्या असतील, तर:
1) बेरीजसाठी गुणधर्म (Addition):
- (a + b) + c = a + (b + c)
- उदाहरण:
- (2 + 3) + 4 = 5 + 4 = 9
- 2 + (3 + 4) = 2 + 7 = 9
- म्हणजेच, (2 + 3) + 4 = 2 + (3 + 4)
2) गुणाकारासाठी गुणधर्म (Multiplication):
- ( a × b ) × c = a × ( b × c )
- उदाहरण:
- ( 2 × 3 ) × 4 = 6 × 4 = 24
- 2 × ( 3 × 4 ) = 2 × 12 = 24
- म्हणजेच, ( 2 × 3 ) × 4 = 2 × ( 3 × 4 )
3) वजाबाकी आणि भागाकर यांना हा गुणधर्म लागू होत नाही.
- उदाहरण:
- ( 10 − 5 ) − 2 = 5 − 2 = 3
- 10 − ( 5 − 2 ) = 10 − 3 = 7
- म्हणून वजाबाकीला हा गुणधर्म लागू नाही.
4. Distributive Property in Marathi :-
एक संख्या दुसऱ्या दोन संख्यांच्या बेरीज किंवा वजाबाकीवर गुणाकार केली, तर ती संख्या दोन्ही संख्यांवर वेगवेगळा गुणाकार करुन उत्तर एकसारखं येतं.
- गुणाकार वरील बेरीजसाठी (Multiplication over Addition):
- a × (b + c) = (a × b) + (a × c)
- उदाहरण:
- 5 × (6 + 2) = 5 × 12 = 60
- (5 × 6) + (5 × 2) = 30 + 10 = 60
- म्हणजेच: 5 × (6 + 2) = (5 × 6) + (5 × 2)
2. गुणाकार वरील वजाबाकीसाठी (Multiplication over Subtraction):
- a × (b – c) = (a × b) – (a × c)
- उदाहरण:
- 5 × (6 – 2) = 5 × 4 = 20
- (5 × 6) – (5 × 2) = 30 – 10 = 20
- म्हणजेच: 5 × (6 – 2) = (5 × 6) – (5 × 2)
संपूर्ण संख्या, पूर्णांक आणि धन संख्यांतील फरक (Whole Numbers vs Integers vs Positive Numbers)
| प्रकार | व्याख्या | उदाहरणे |
|---|---|---|
| पूर्ण संख्या (W) | 0 आणि सर्व धन पूर्णांक | 0, 1, 2, 3, 4, 5, … |
| पूर्णांक (Z) | सर्व धन पूर्णांक, 0, आणि ऋण पूर्णांक | … -3, -2, -1, 0, 1, 2… |
| धन संख्या | 0 सोडून फक्त सर्व धन पूर्णांक | 1, 2, 3, 4, 5… |
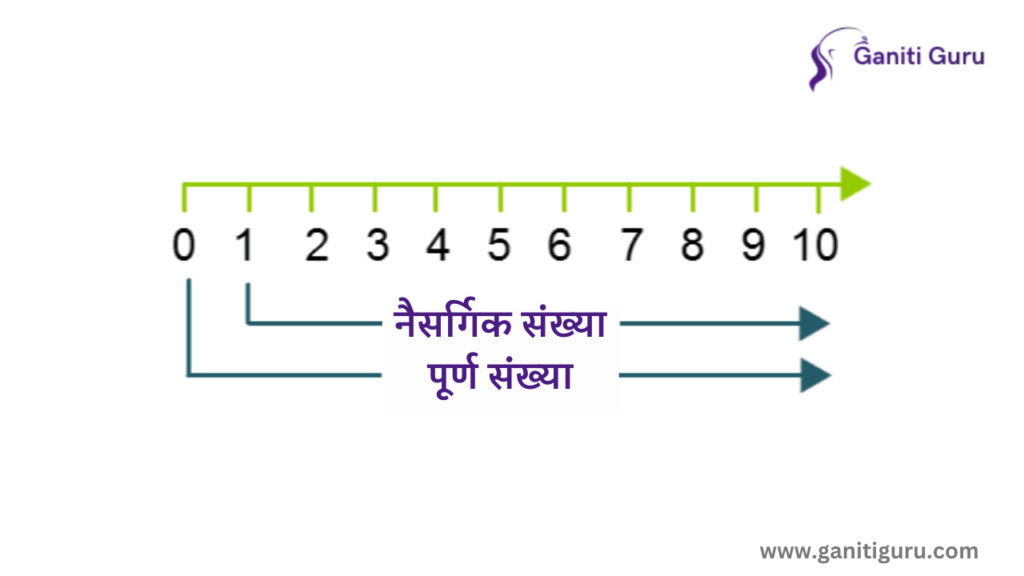
पूर्ण संख्यांचे महत्वाचे मुद्दे (Key Points about Whole Numbers in Marathi)
- पूर्ण संख्या म्हणजे काय?
- शून्य (0) पासून सुरू होणाऱ्या आणि धन पूर्णांकांचा समुह म्हणजे पूर्ण संख्या होय.
- उदा. 0, 1, 2, 3, 4, 5, …
- पूर्ण संख्या याचे चिन्ह:
Wहे पूर्ण संख्यांचे प्रतीक आहे.- W = {0, 1, 2, 3, 4, 5, …}
- शून्य (0) ही सर्वात लहान पूर्ण संख्या आहे.
- पूर्ण संख्या ही अपुर्णांक (Fractions) किंवा दशांश (Decimals) नसते.
- प्रत्येक नैसर्गिक संख्या ही एक पूर्ण संख्या असते, पण सर्व पूर्ण संख्या नैसर्गिक नसतात (उदा. 0).
- पूर्ण संख्यांमध्ये ऋण संख्या (Negative numbers) नसतात.
- पूर्ण संख्या या वास्तविक संख्यांचा (Real Numbers) भाग आहेत.
- पूर्ण संख्यांचा उपयोग रोजच्या जीवनातील मोजणी, मोजमाप, गणना यासाठी होतो.
पूर्ण संख्या (Whole Numbers) – वारंवार विचारले जाणारे प्रश्न (FAQs)
Q1: पूर्ण संख्या म्हणजे काय?
उत्तर: पूर्ण संख्या म्हणजे अशा संख्यांचा समुह जो 0 पासून सुरुवात होतो आणि पुढे फक्त सकारात्मक पूर्णांक असतात.
उदा. 0, 1, 2, 3, 4, …
Q2: शून्य (0) ही पूर्ण संख्या आहे का?
उत्तर: होय, शून्य ही पहिली व सर्वात लहान पूर्ण संख्या आहे.
Q3: नैसर्गिक संख्या आणि पूर्ण संख्येमध्ये काय फरक आहे?
उत्तर: नैसर्गिक संख्यांमध्ये 1 पासून सुरुवात होते (1, 2, 3, …), तर पूर्ण संख्यांमध्ये 0 पासून सुरुवात होते (0, 1, 2, 3, …). त्यामुळे प्रत्येक नैसर्गिक संख्या ही पूर्ण असते, पण प्रत्येक पूर्ण संख्या नैसर्गिक नाही.
Q4: पूर्ण संख्यांची सर्वात मोठी संख्या कोणती आहे?
उत्तर: पूर्ण संख्यांना शेवट नाही, कारण त्या अनंतपर्यंत जातात.
निष्कर्ष (Conclusion) :-
पूर्ण संख्या ही गणितातील एक मूलभूत आणि अत्यंत उपयुक्त संकल्पना आहे. शून्यासह सुरू होणाऱ्या आणि पुढे जाणाऱ्या सर्व नैसर्गिक संख्यांचा समावेश पूर्ण संख्यांमध्ये होतो. यामध्ये कोणताही अपूर्णांक, दशांश किंवा ऋण संख्या नसते. पूर्ण संख्यांचे विविध गुणधर्म यामुळे गणितातील विविध संक्रियांना सुलभता प्राप्त होते.
ही संकल्पना विद्यार्थ्यांना संख्यांचे प्रकार, त्यांचे व्यवहार आणि संख्यात्मक तर्कशक्ती यांचा खोल अभ्यास करण्यासाठी आवश्यक आहे.
त्यामुळे अभ्यास करताना पूर्ण संख्यांचे नियम, गुणधर्म आणि त्यावर आधारित उदाहरणे लक्षात ठेवणे अत्यंत महत्त्वाचे आहे.
अधिक सरावासाठी गणितगुरु (Ganitiguru.com) या ब्लॉगला नियमित भेट द्या आणि गणितातील विविध संकल्पना सुलभ भाषेत समजून घ्या.
“गणित सोपा करायला आम्ही येथे आहोत!”
गणितिगुरुला टेलीग्रामवर फॉलो करा


