आकृत्यांच्या संख्या मोजणे | Counting Figures in Marathi

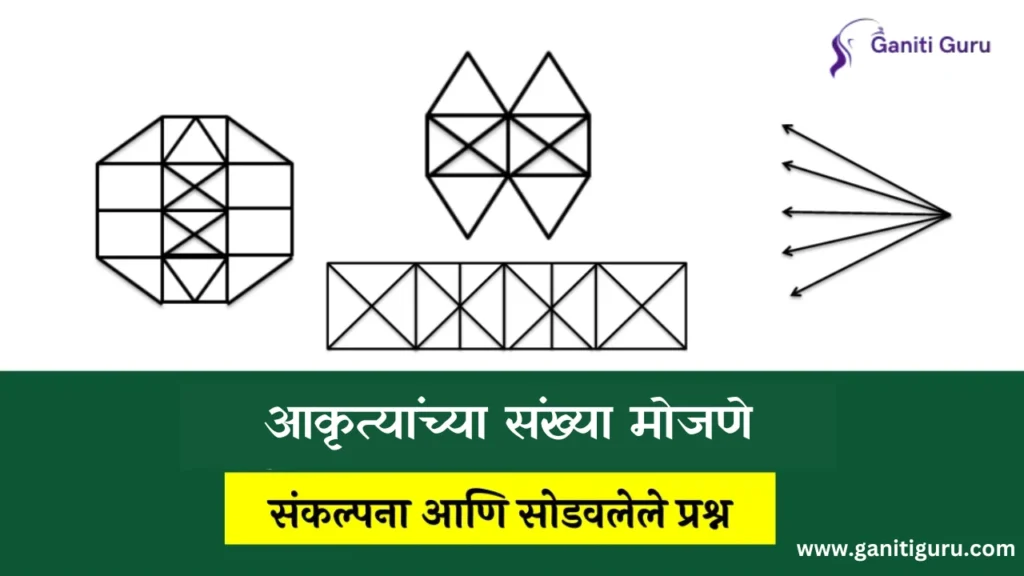
स्पर्धा परीक्षांमध्ये विचारले जाणारे तर्कशक्तीवर आधारित प्रश्नांपैकी “आकृत्यांची संख्या मोजणे | Counting Figures in Marathi“ हा एक महत्त्वाचा प्रकार आहे. अशा प्रश्नांमध्ये आपल्याला एक आकृती दिली जाते आणि त्यामध्ये रेषा, कोन, त्रिकोण, चौरस किंवा आयत किती आहेत हे ओळखून मोजावे लागते. सुरुवातीला हे प्रश्न सोपे वाटू शकतात, परंतु त्यामागील नियम आणि युक्त्या समजल्या नाहीत तर चुका होण्याची शक्यता जास्त असते. म्हणूनच या लेखात आपण फक्त दोन महत्त्वाच्या गोष्टींचा अभ्यास करणार आहोत:

1. रेषांची संख्या मोजणे – आडव्या, उभ्या आणि तिरक्या रेषांची योग्य प्रकारे मोजणी कशी करायची, हे उदाहरणासह समजून घेऊ.
2. कोनांची संख्या मोजणे – दिलेल्या आकृतीत एकूण कोन किती आहेत आणि त्यांची वर्गवारी कशी करायची, हे सविस्तर पाहणार आहोत.

जर तुम्हाला हे प्रश्न सोडवताना अडचण येत असेल, तर ह्या लेखातील सोप्या पद्धती, स्टेप-बाय-स्टेप मार्गदर्शन आणि उदाहरणे तुम्हाला निश्चितच उपयुक्त ठरतील.

आकृत्यांच्या संख्या मोजणे | Counting Figures in Marathi

दिलेल्या आकृती मधील आकृत्यांची संख्या मोजणे कधीकधी खूप कठीण वाटते जर तुम्हाला ते कसे सोडवायचे याची कल्पना नसेल तर या लेखात, आम्ही तुम्हाला आकृती मोजण्याच्या युक्त्यांबद्दल माहिती देणार आहोत. आकृत्यांची मोजणी हे सर्वात जास्त वारंवार विचारले जाणारे तर्क प्रश्न आहेत. यामध्ये, आपल्याला एक आकार किंवा आकृती दिली जाईल आणि आपले कार्य आकार निश्चित करणे आणि त्या विशिष्ट आकारात मोजणे आहे.

उदाहरणार्थ, खालील आकृतीचा विचार करा:

दिलेल्या आकृतीत किती त्रिकोण दिसतात? सुरुवातीला, हे कदाचित सोपे वाटेल परंतु ते नक्कीच नाही! युक्त्या जाणून घेतल्याशिवाय आपण अचूक उत्तर सहज काढू शकत नाही. चला तर मग जाणून घेऊया,

1.कोनांची संख्या मोजणे (Counting Angles in Marathi)

कोन म्हणजे काय? (What is an Angle in Marathi)

कोन म्हणजे दोन किरण (रेषा) एका सामान्य बिंदूवर एकत्र आले की जे तयार होतो तो कोन (Angle) होय.

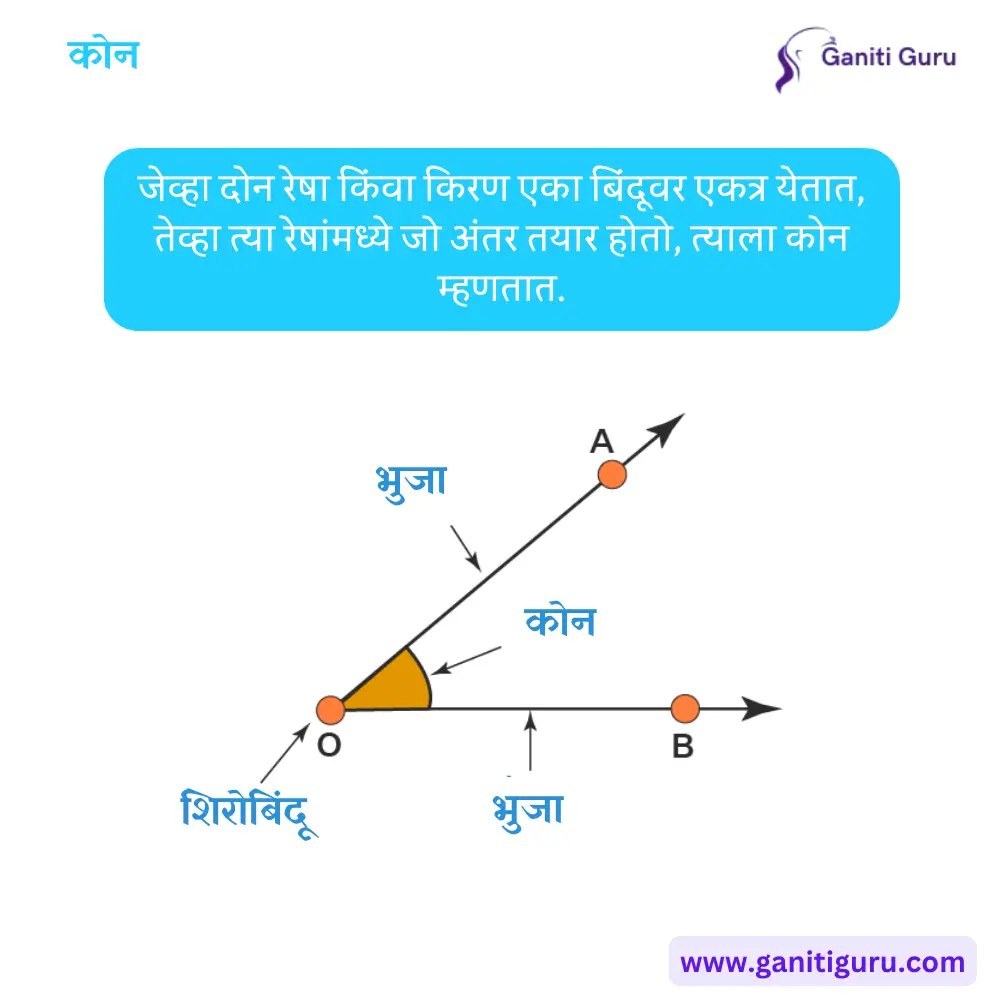
कोनांची संख्या मोजणे :-

• दिलेल्या आकृतीत बाणाच्या एकूण संख्येमधून 1 वजा करून, नंतर उरलेल्या बाणांच्या संख्येची उतरत्या क्रमाने बेरीज करा. ही प्रक्रिया खालीलप्रमाणे आहे:
• सूत्र:
  • जर एकूण बाणांची संख्या = n असेल तर,
  • उरलेल्या बाणांची संख्या = n – 1 आणि
  • त्यांची उतरत्या क्रमाने बेरीज = (n – 1) × n ÷ 2
  • म्हणजे:
  • एकूण कोनाची संख्या = (n – 1) × n / 2

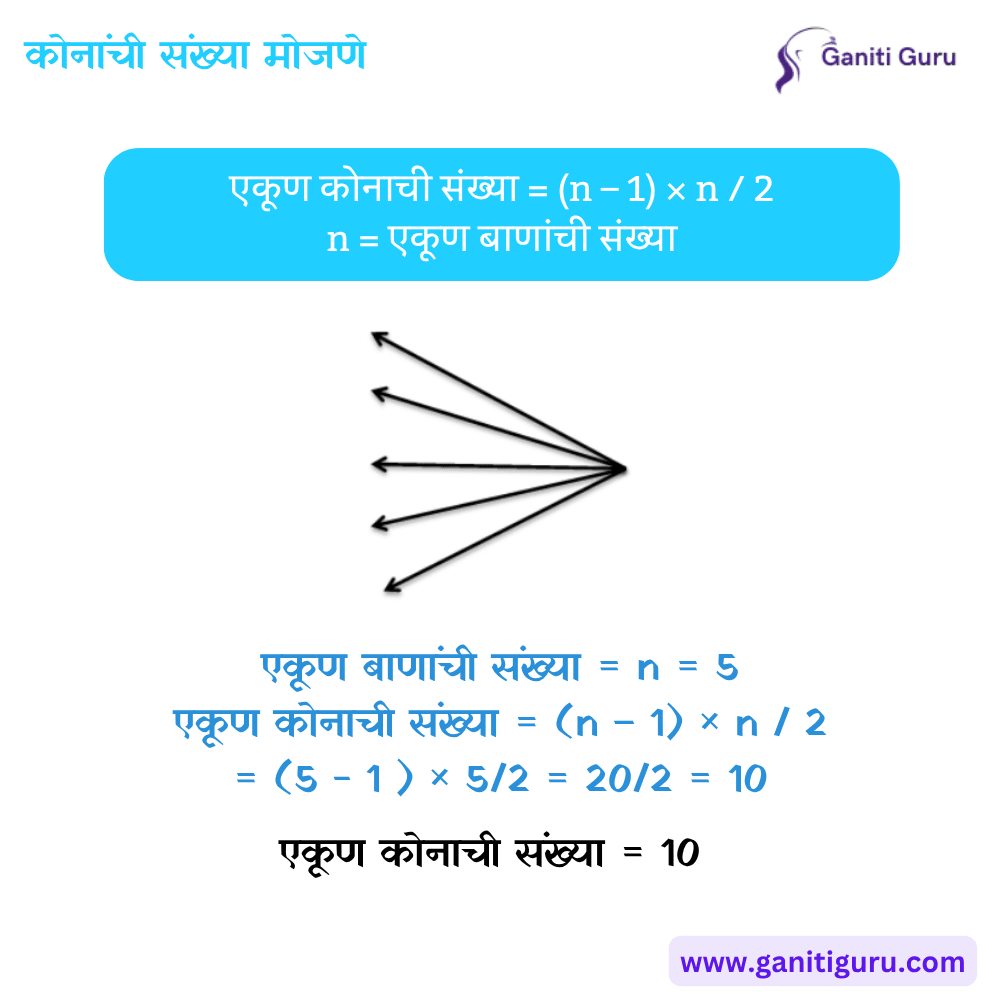
1.रेषांची संख्या मोजणे (Counting Straight Lines in Marathi)

रेषा म्हणजे काय? (What is an Straight Lines in Marathi)

रेषा म्हणजे बिंदूंच्या सतत चालू राहणाऱ्या मालिकेने तयार झालेली एक सरळ लांब आकृती होय. ती अंतहीन असते आणि दोन टोकांमधून सरळ रेषेत वाढत राहते.

रेषेचे प्रकार:

1. संपूर्ण रेषा (Line) – जी दोन्ही बाजूंना अनंतपर्यंत वाढते.
2. रेषाखंड (Line Segment) – ज्याला सुरुवात व शेवटचे निश्चित बिंदू असतात.
3. किरण (Ray) – ज्याला एक निश्चित प्रारंभबिंदू असतो आणि दुसऱ्या बाजूला ती अनंतपर्यंत वाढते.

रेषांची संख्या मोजणे :-

दिलेल्या आकृतीतील रेषांची संख्या मोजताना आपण खालील क्रमाने मोजणी करावी:

1. आडव्या रेषा (Horizontal Lines) – वरून खाली एकेका थरात किती रेषा आहेत ते पहा.
2. उभ्या रेषा (Vertical Lines) – डावीकडून उजवीकडे सरळ रेषा किती आहेत ते मोजा.
3. तिरप्या रेषा (Inclined / Slant Lines) – ज्या रेषा आडव्या-उभ्या नसून झुकलेल्या आहेत, त्यांची नोंद घ्या.

सूत्र : एकूण रेषा = आडव्या रेषा + उभ्या रेषा + तिरप्या रेषा

टीप:

• प्रत्येक वेगळी रेषा फक्त एकदाच मोजावी.
• रेषा ज्या दोन बिंदूंना जोडते, त्यावर लक्ष द्या.

निष्कर्ष (Conclusion)

आकृत्यांतील रेषा आणि कोनांची संख्या मोजणे हे गणितातील तसेच तर्कशक्ती तपासणाऱ्या प्रश्नांमध्ये खूप महत्त्वाचे कौशल्य आहे. या प्रकारच्या प्रश्नांसाठी योग्य निरीक्षण, निश्चित क्रम आणि पद्धतशीर मोजणी आवश्यक असते. जर आपण रेषांचे प्रकार (आडव्या, उभ्या, तिरक्या) आणि कोन तयार होण्याचे नियम नीट लक्षात घेतले, तर कोणतीही आकृती सोपेपणाने विश्लेषित करता येते. स्पर्धा परीक्षा, शालेय अभ्यासक्रम, किंवा बौद्धिक कौशल्य वाढवण्यासाठीही आकृती मोजणे हे एक उपयुक्त आणि मनोरंजक क्षेत्र आहे. योग्य पद्धतीने विचार आणि सराव केल्यास तुम्ही कोणतीही आकृती आत्मविश्वासाने सोडवू शकता!

तुम्हाला आवडत असेल तर अशा आणखी गणिताच्या ट्रिक्स, सुलभ पद्धती, आणि संकल्पना मराठीतून शिकण्यासाठी GanitiGuru ला भेट द्या!

गणितिगुरुला टेलीग्रामवर फॉलो करा