आकृत्यांच्या संख्या मोजणे – चौरसांची व आयतांची संख्या मोजणे | Counting of Squares and Rectangles in Marathi

चौरसांची व आयतांची संख्या मोजणे | Counting of Squares and Rectangles in Marathi

Counting of Squares and Rectangles in Marathi :- स्पर्धा परीक्षा, बुद्धिमत्ता चाचण्या आणि विविध निवड प्रक्रियांमध्ये आकृत्यांच्या मोजणीवर आधारित प्रश्न विचारले जातात. त्यामध्ये चौरस आणि आयत यांची संख्या मोजणे हे एक अत्यंत सामान्य आणि महत्त्वाचे गणितीय कौशल्य आहे. खालील लेखात आपण आकृती ओळखून, त्यातील चौरस व आयत नेमकेपणाने कसे मोजायचे, हे विविध उदाहरणे, प्रकार व युक्त्यांसह शिकणार आहोत. हे समजून घेतल्यास तुम्हाला अशा प्रकारचे प्रश्न सोडवणे अधिक सोपे आणि वेगवान होईल!

चौरसांची संख्या मोजणे | Counting of Squares in Marathi :-

चौरस म्हणजे काय?

चौरस (Square) ही एक अशी चतुर्भुज आकृती आहे ज्याच्या सर्व बाजू समान लांबीच्या असतात आणि सर्व कोन 90 अंशाचे (right angle) असतात.

चौरसाची मुख्य वैशिष्ट्ये:

• 4 बाजू असतात — सर्व बाजूंची लांबी एकसारखी असते.
• 4 कोन असतात — प्रत्येक कोन 90 अंशाचा असतो.
• 2 समांतर रेषा जोड्या असतात — समोरील बाजू एकमेकांना समांतर असतात.
• 2 कर्ण (diagonals) — त्या एकमेकींना समकोणात छेदतात व समान लांबीच्या असतात.

चौरसांची संख्या मोजणे | Counting Squares in Marathi :-

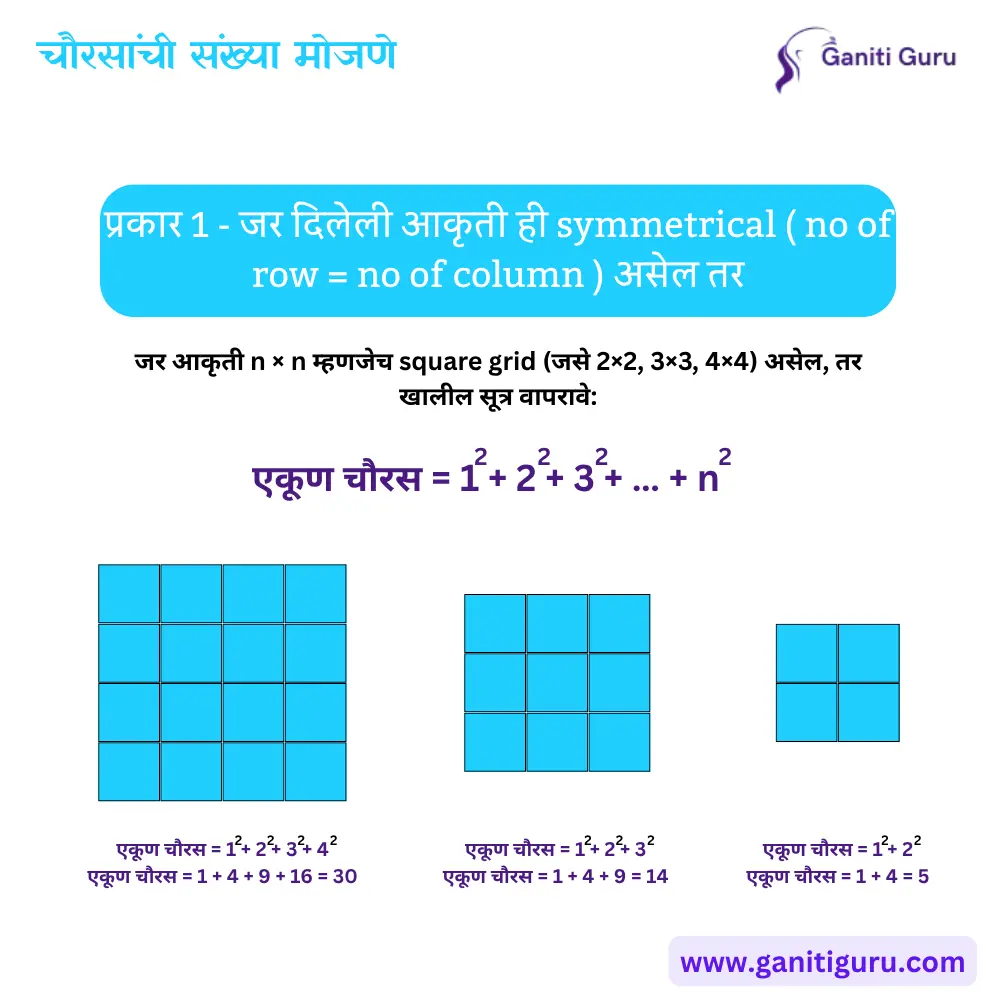
प्रकार 1 – आकृती जर Symmetrical ( No of row = No of column ) असेल तर

जर आकृती n × n म्हणजेच square grid (जसे 2×2, 3×3, 4×4) असेल, तर खालील सूत्र वापरावे:

सूत्र: एकूण चौरस = 1² + 2² + 3² + … + n²

उदाहरण : 3 × 3 आकृतीमध्ये:

• 1² + 2² + 3² = 1 + 4 + 9 = 14 चौरस

प्रकार 2 – आकृती जर Non Symmetrical ( No of row ≠ No of column ) असेल तर

जेव्हा Row आणि Column समान नसतात (उदा. 3×4, 2×5 इ.), तेव्हा फक्त square आकृती मोजण्यासाठी आपण सर्व शक्य असलेल्या समदिशा चौरसांचा विचार करतो.

उदाहरण 1 : 2 × 3 आकृतीमध्ये:

• 1 × 1 चौरस = 2 × 3 = 6
• 2 × 2 चौरस = 1 × 2 = 2
• एकूण चौरस = 6 + 2 = 8

उदाहरण 2: 3 × 4 आकृतीमध्ये:

• 1 × 1 चौरस = ( 3 × 4 ) = 12
• 2 × 2 चौरस = ( 2 × 3 ) = 6
• 3 × 3 चौरस = ( 1 × 2 ) = 2
• 4 × 4 शक्य नाही (कारण 3 rows आहेत)
• एकूण चौरस = 12 + 6 + 2 = 20 चौरस

आयतांची संख्या मोजणे | Counting of Rectangles in Marathi :-

आयत म्हणजे काय?

आयत (Rectangle) ही एक चौकोनी आकृती आहे ज्यामध्ये समोरासमोरच्या बाजू समांतर आणि लांबीने समान असतात. आयताच्या चारही कोनांची मापे 90 अंश असतात.

आयताची वैशिष्ट्ये:

1. चार बाजू असतात – दोन लांब (Length) आणि दोन रुंद (Breadth).
2. चार कोन असतात – सर्व कोन समकोण (90°) असतात.
3. समोरासमोरच्या बाजू समांतर आणि समान लांबीच्या असतात.
4. आयताचे क्षेत्रफळ = लांबी × रुंदी.

आयतांची संख्या मोजणे | Counting of Rectangles in Marathi :-

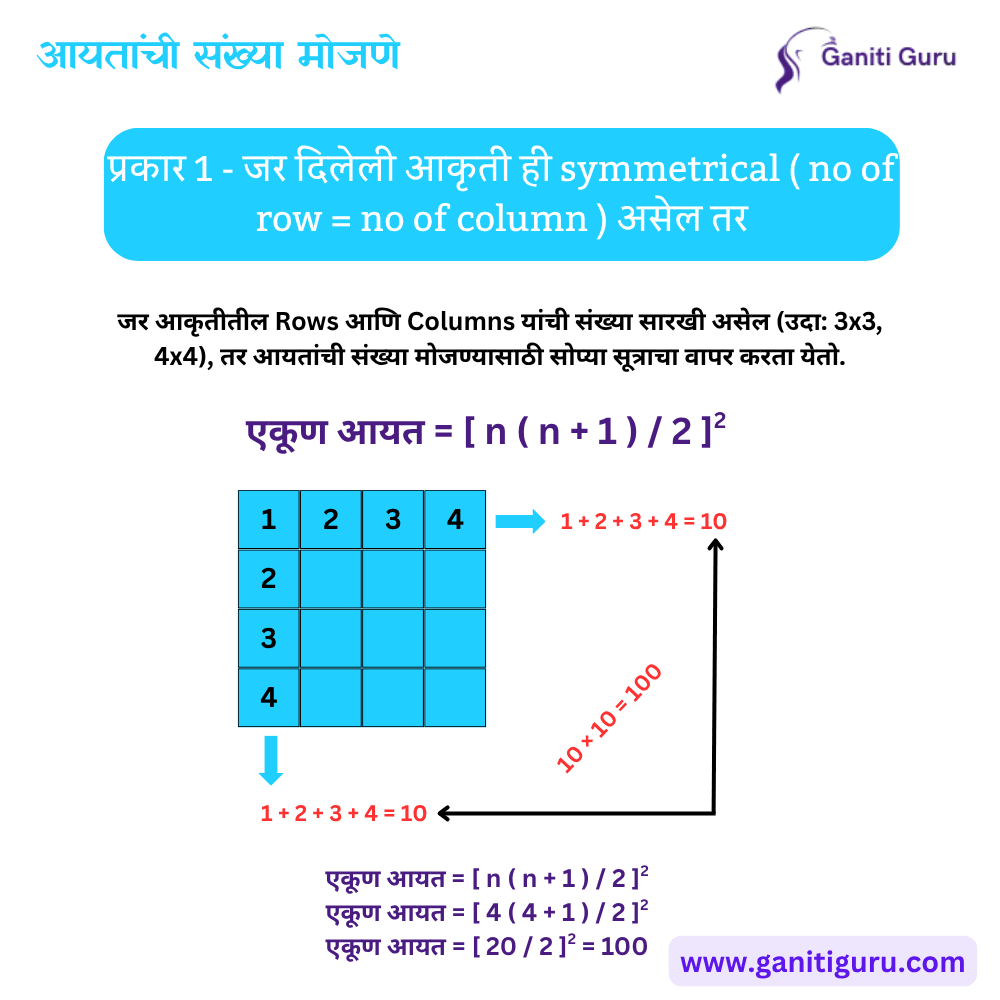
प्रकार 1 – आकृती जर Symmetrical ( No of row = No of column ) असेल तर

जर आकृतीतील Rows आणि Columns यांची संख्या सारखी असेल (उदा: 3×3, 4×4), तर आयतांची संख्या मोजण्यासाठी सोप्या सूत्राचा वापर करता येतो.

सूत्र: एकूण आयत = [ n ( n + 1 ) / 2 ]²

उदाहरण 1 : 3 × 3 आकृतीमध्ये:

• एकूण आयत = [ 3 ( 3 + 1 ) / 2 ]²
• एकूण आयत = [ 12 / 2 ]² = 6² = 36

उदाहरण 2 : 4 × 4 आकृतीमध्ये:

• एकूण आयत = [ 4 ( 4 + 1 ) / 2 ]²
• एकूण आयत = [ 20 / 2 ]² = 10² = 100

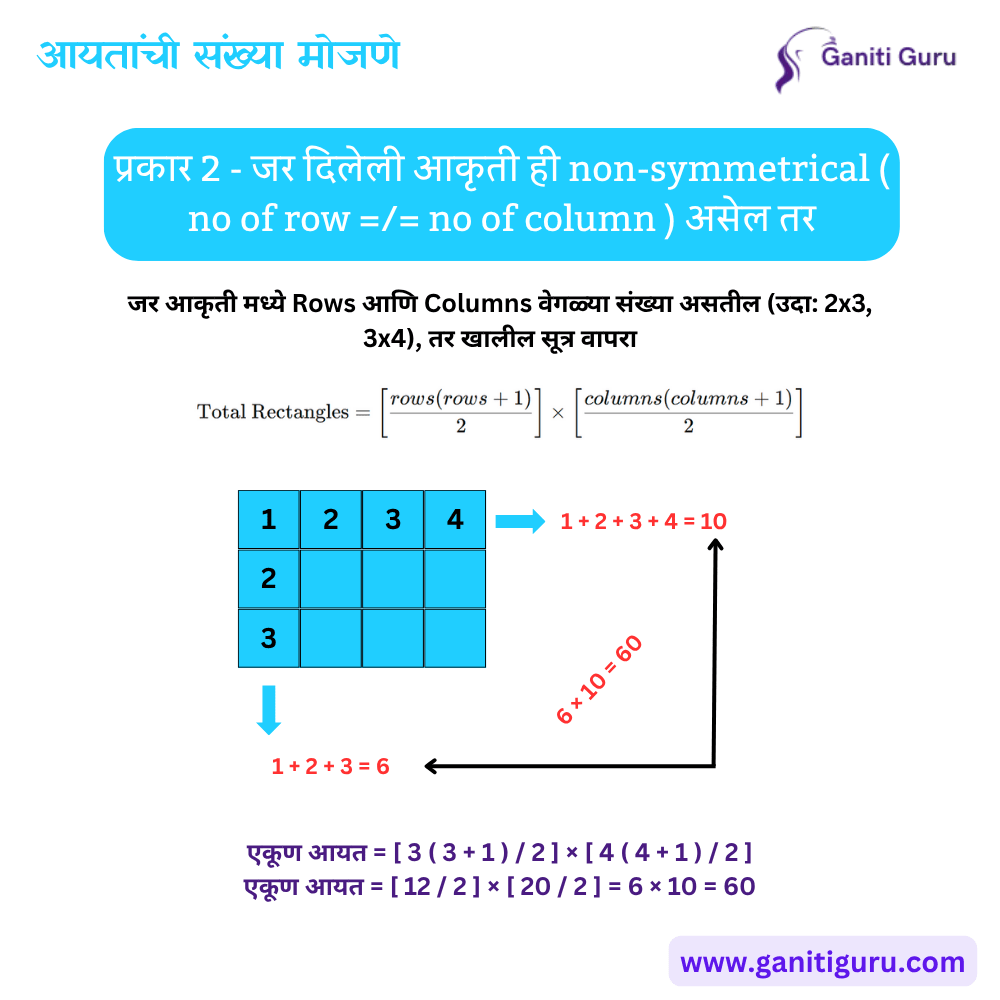
प्रकार 2 – आकृती जर Non Symmetrical ( No of row ≠ No of column ) असेल तर

जर आकृती मध्ये Rows आणि Columns वेगळ्या संख्या असतील (उदा: 2×3, 3×4), तर खालील सूत्र वापरा:

सूत्र: एकूण आयत = [ rows ( rows + 1) /2 ] × [ columns ( columns + 1) /2 ]

उदाहरण 1 : 2 × 3 आकृतीमध्ये:

• एकूण आयत = [ 2 ( 2 + 1 ) / 2 ] × [ 3 ( 3 + 1 ) / 2 ]
• एकूण आयत = [ 6 / 2 ] × [ 12 / 2 ] = 3 × 6 = 18

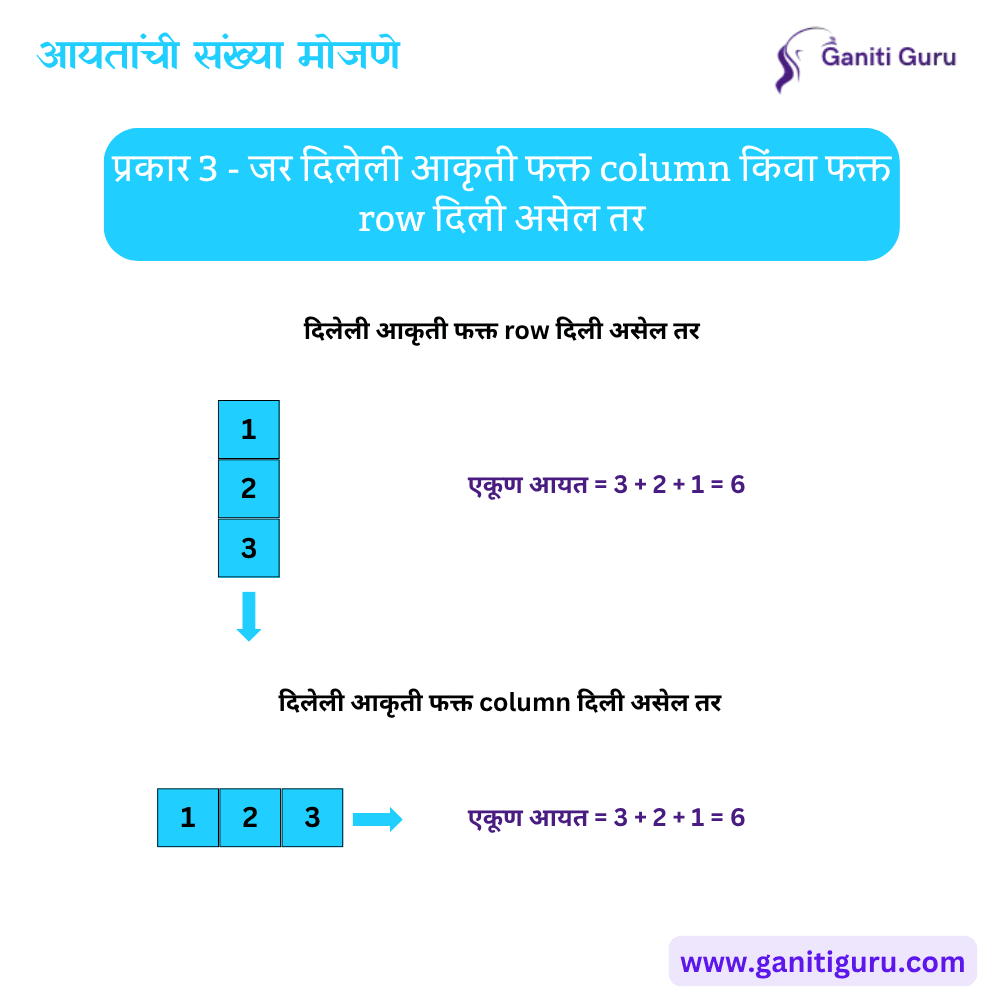
प्रकार 3 – जर दिलेली आकृती फक्त column किंवा फक्त row दिली असेल तर

निष्कर्ष:

चौरस आणि आयतांची मोजणी करताना जर योग्य सूत्र, विश्लेषण व निरीक्षण वापरले, तर अगदी जटिल आकृतीतही अचूक मोजणी करणे शक्य होते. अभ्यास व सरावाने अशा प्रकारचे प्रश्न सोडवणे सोपे जाते आणि स्पर्धा परीक्षांमध्ये अधिक गुण मिळण्यास मदत होते.

हवे असल्यास तुम्हाला यासाठी वर्कशीट, उदाहरणे किंवा व्याख्येसह तक्तेही देऊ शकतो.

GanitiGuru – तुमच्या गणित अभ्यासाचा विश्वासू मार्गदर्शक!

गणितिगुरुला टेलीग्रामवर फॉलो करा