आकृत्यांमधील त्रिकोणांची संख्या कशी मोजावी? | Counting Triangles in Marathi

आकृत्यांमधील त्रिकोण मोजणे | Counting Triangles in Marathi :- हे गणितात एक मनोरंजक पण चकवा देणारे प्रकरण आहे. स्पर्धा परीक्षा, बुद्धिमत्ता चाचण्या किंवा मुलांच्या अभ्यासक्रमात अशा प्रश्नांची नेहमीच उपस्थिती असते. बर्‍याचदा एक आकृती दिली जाते आणि विचारले जाते — “या आकृतीमध्ये किती त्रिकोण आहेत?“. पहिल्या नजरेत हा प्रश्न सोपा वाटतो, पण खरी अडचण अचूक मोजण्यात असते. या ब्लॉगमध्ये आपण अशा आकृतीमधून त्रिकोणांची संख्या कशी मोजायची, कोणते युक्तीवाद वापरायचे, आणि वेगवेगळ्या प्रकारांचे विश्लेषण कसे करायचे हे समजून घेणार आहोत.

त्रिकोण म्हणजे काय?

• त्रिकोण ही एक बंद आकृती आहे जी तीन सरळ रेषांपासून बनलेली असते.
• त्रिकोणात असणाऱ्या तीन कोनांची बेरीज नेहमी 180 अंश (degree) असते.
• जर एखाद्या त्रिकोणाचे शिरोबिंदू P, Q, आणि R असतील तर तो त्रिकोण △PQR अशा चिन्हाने दर्शवतात.

मुख्य प्रकार – त्रिकोण मोजण्याचे प्रकार (Counting Triangles in Marathi)

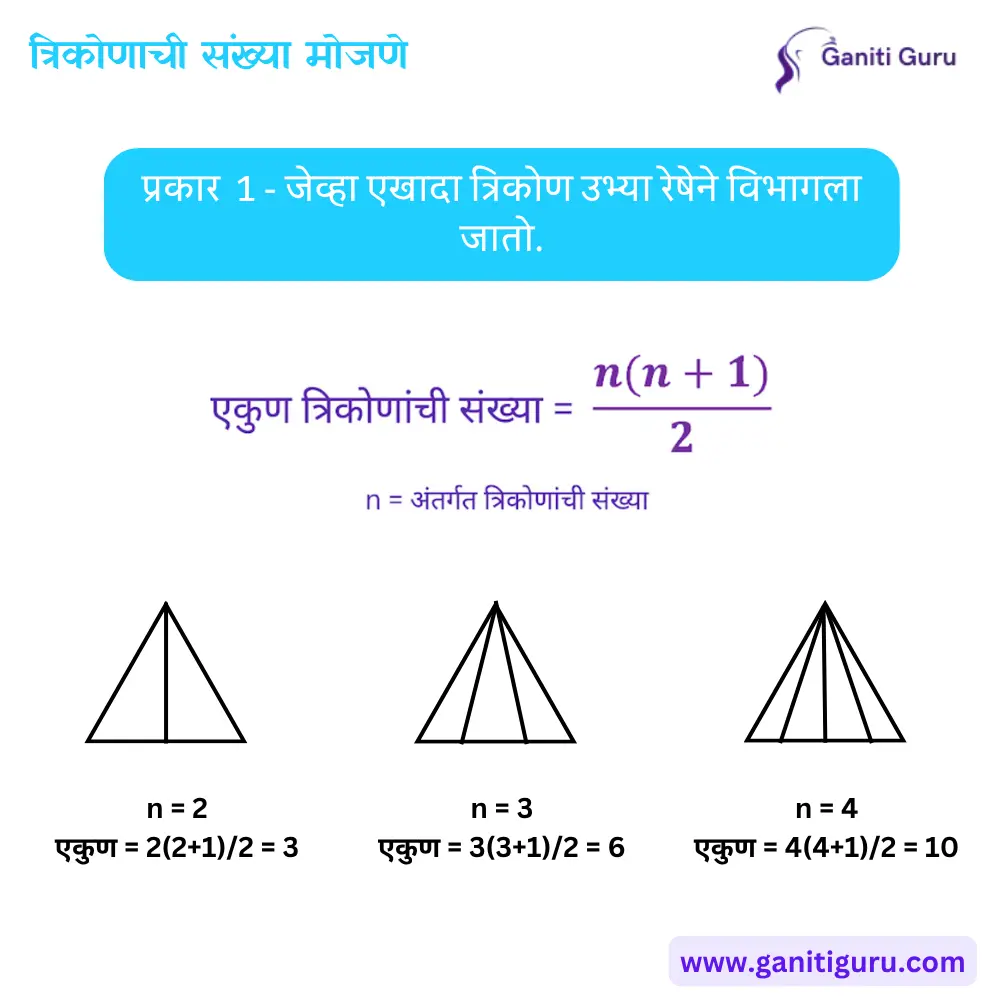
1. उभ्या रेषांमुळे विभागलेला त्रिकोण (Vertical Lines Division) :-

• त्रिकोण एका बाजूने उभ्या रेषांनी विभागलेला असतो.
• यामध्ये त्रिकोणाच्या एका बाजूवर अनेक रेषा जातात आणि प्रत्येक विभाग नवीन त्रिकोण निर्माण करतो.
• सूत्र:
  • एकूण त्रिकोण = n(n+1)​/2
    • n = अंतर्गत त्रिकोणाची संख्या

2.आडव्या रेषांमुळे विभागलेला त्रिकोण (Horizontal Lines Division)

• त्रिकोणाच्या आतील भाग आडव्या रेषांनी विभागलेला असतो.
• सूत्र:
  • एकूण त्रिकोण = एकूण आडव्या रेषा (m)
    • m = आडव्या रेषा

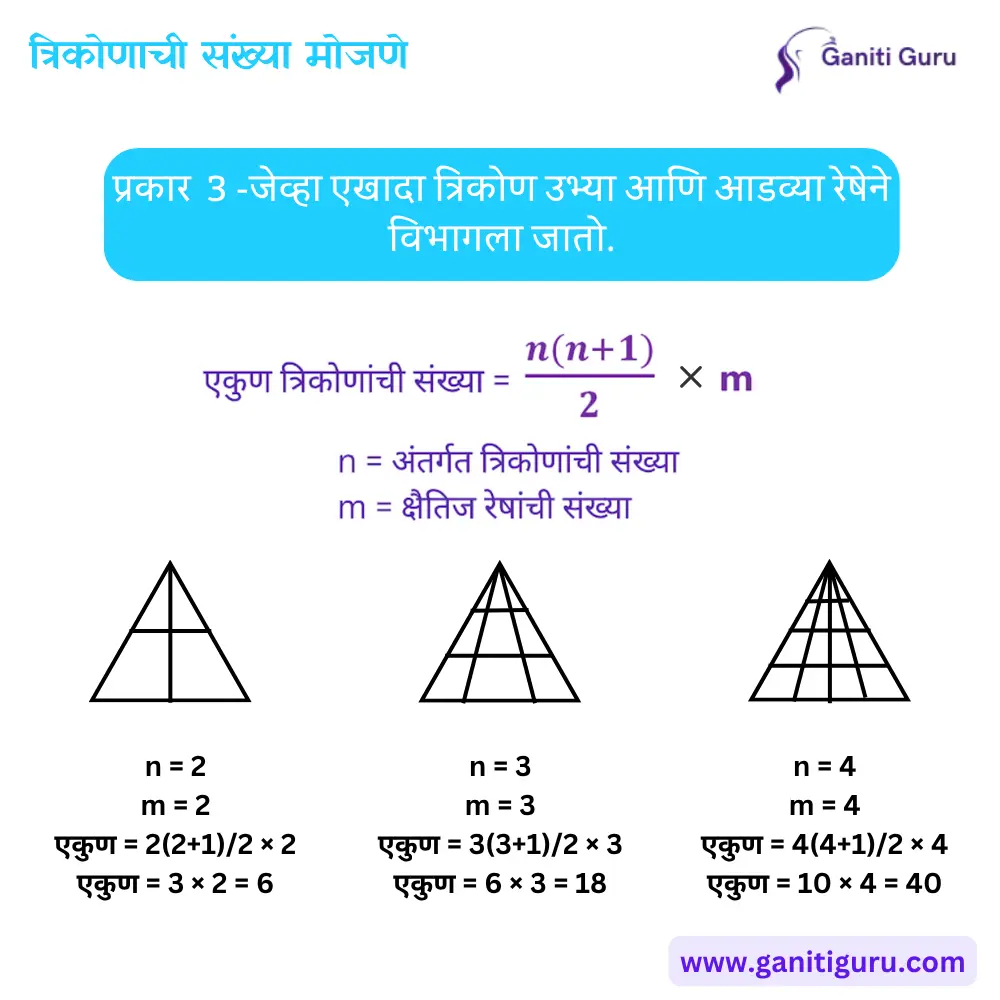
3.उभ्या व आडव्या दोन्ही रेषांनी विभागलेला त्रिकोण (When Triangle has both Vertical and Horizontal Lines )

• त्रिकोणाच्या आतील भाग उभ्या व आडव्या रेषांनी विभागलेला असतो.
• सूत्र:
  • एकूण त्रिकोण = एकूण आडव्या रेषा (m) × n(n+1)​/2
    • m = आडव्या रेषा
    • n = अंतर्गत त्रिकोणाची संख्या

4. त्रिकोणाच्या आतील त्रिकोण (Triangle inside Triangle)

• मोठ्या त्रिकोणाच्या आत छोटा त्रिकोण दिसतो.
• आतला त्रिकोण बाहेरील त्रिकोणाच्या तीनही बाजूंना स्पर्श करतो.
• सूत्र:
  • एकूण त्रिकोण = 5

5. त्रिकोणाच्या आतील त्रिकोण (Triangle inside Triangle)

• जेव्हा त्रिकोणाच्या बाहेरील सर्व कडांना स्पर्श करणारा त्रिकोण असतो आणि मुख्य त्रिकोणाच्या प्रत्येक शिरोबिंदूच्या आतील बाजूच्या कडा स्पर्श करणाऱ्या रेषा असतात.
  • Step i – सर्वप्रथम त्रिकोणाच्या कोपऱ्यातून येणाऱ्या सर्व रेषांकडे दुर्लक्ष करा
  • Step ii – आता तुम्हाला दिसणारा त्रिकोण मागील केसमधील त्रिकोणासारखा असेल (बाह्य त्रिकोणाच्या सर्व कडा स्पर्श करणे).
  • Step iii – त्रिकोणाची संख्या मोजा
    त्रिकोणांची संख्या = 4 + 1 = 5
  • Step iv – यानंतर काठावरून येणाऱ्या रेषांचा विचार करा, प्रत्येक रेषा २ त्रिकोण बनवेल
    त्रिकोणांची संख्या = 3 x 2 = 6
  • Step v – आता ते सर्व एकत्र जोडा
    एकुण त्रिकोणांची संख्या = 5 + 6 = 11

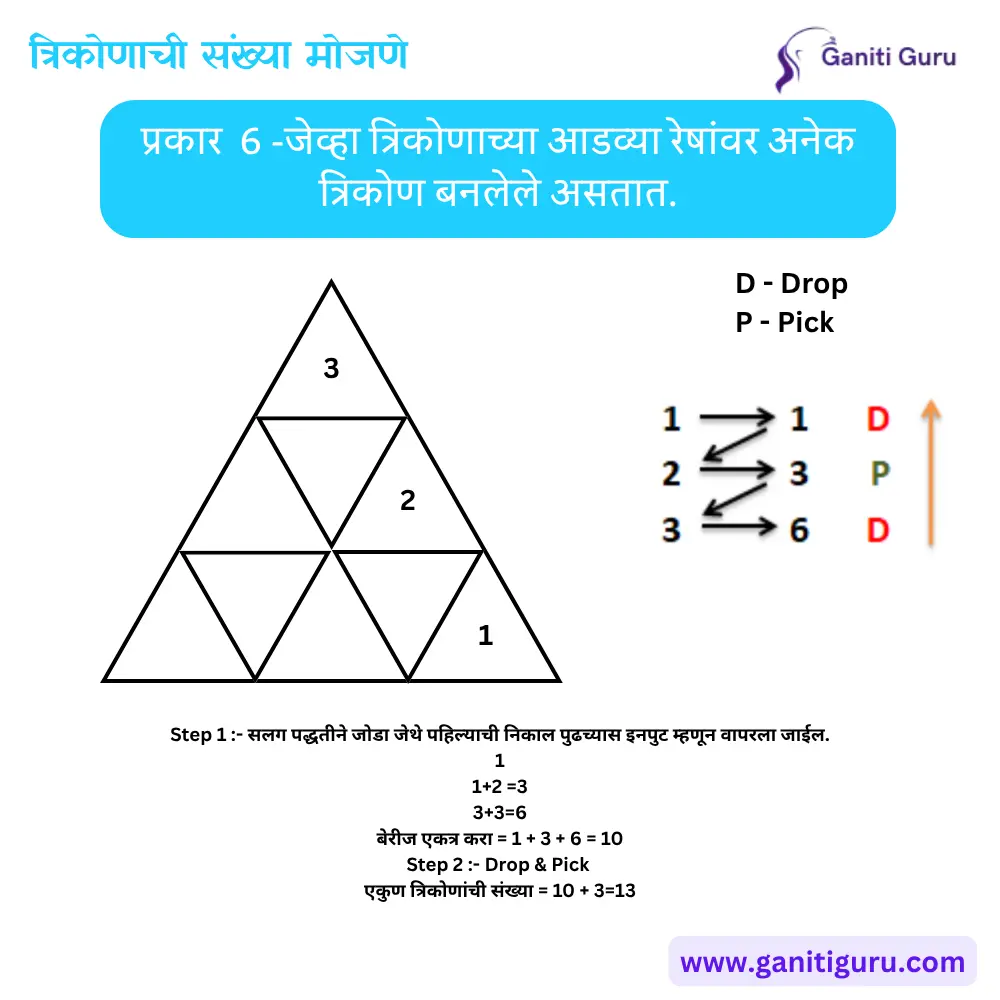
6. सममित आकृतीतील त्रिकोण (Symmetric Figures)

• सममितीच्या आधारावर त्रिकोणांची संख्या मोजावी लागते.
• उदाहरणार्थ, एक मोठा त्रिकोण अनेक सममित त्रिकोणांनी बनलेला असतो.
  • Step 1 : जर तुम्ही प्रत्येक काठावरुन बारकाईने पाहिले तर तळापासून समान त्रिकोण दिसतील.
  • Step 2 : पाया पासुन त्रिकोण मोजा
  • Step 3 : त्यांना सलग पद्धतीने जोडा जेथे पहिल्याची निकाल पुढच्यास इनपुट म्हणून वापरला जाईल.
  • Step 4 : म्हणजेच 1, 1 +2 = 3, 3+3 = 6, 4+6 = 10 ‘. सर्व बेरीज एकत्र करा.
  • Step 5 : Drop and Pick” वापरून = 10 + 3 = 13

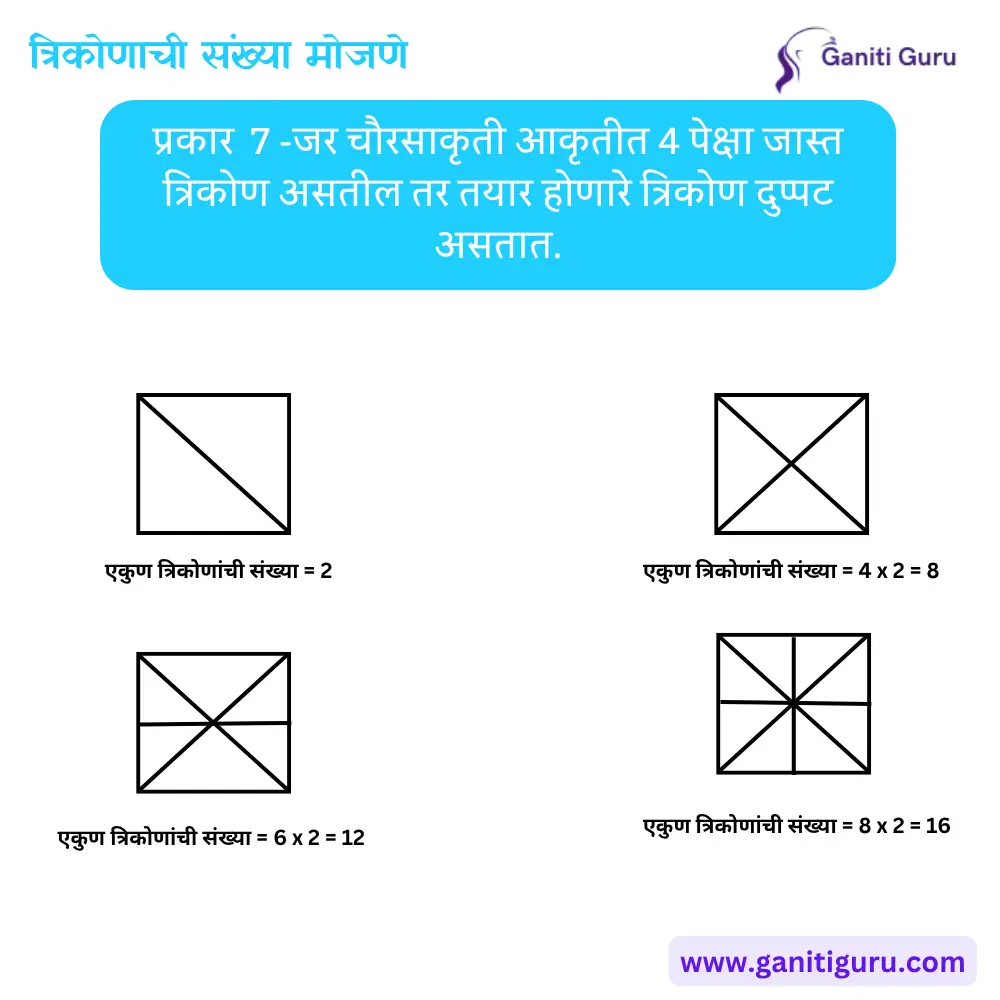
7. बंद आकृतीमधील त्रिकोण (Closed Figures)

• चौरस किंवा इतर बंद आकृतीत केलेल्या रेषांमुळे त्रिकोण तयार होतात.
• सूत्र:
  • जर चौरसाकृती आकृतीत 4 पेक्षा जास्त त्रिकोण असतील तर तयार होणारे त्रिकोण दुप्पट असतात.

8. मध्यबिंदूपासून येणाऱ्या रेषांमुळे विभागलेले त्रिकोण

• त्रिकोणाच्या मध्याकापासून आतील बाजूस जर 6 त्रिकोण तयार होत असेल तर त्या आकृती मध्ये एकुण 16 त्रिकोण तयार होतात.

निष्कर्ष (Conclusion):

त्रिकोण मोजणे हे त्रासदायक वाटू शकते, पण एकदा का तुम्हाला प्रकार आणि युक्ती समजल्या, की हे खूप सोपे आणि मजेदार होऊन जाते. स्पर्धा परीक्षा आणि बुद्धिमत्ता चाचण्यांमध्ये वेळ वाचवण्यासाठी ही कौशल्य खूप महत्त्वाची आहे.

तुम्हाला आवडत असेल तर अशा आणखी गणिताच्या ट्रिक्स, सुलभ पद्धती, आणि संकल्पना मराठीतून शिकण्यासाठी GanitiGuru ला भेट द्या!

गणितिगुरुला टेलीग्रामवर फॉलो करा