Ratio and Proportion Shortcut Tricks in Marathi :- गणितातील सर्वात मूलभूत आणि महत्त्वाचा विषय म्हणजे “गुणोत्तर आणि प्रमाण”. स्पर्धा परीक्षा, शालेय अभ्यासक्रम तसेच व्यवहारातील अनेक गणनांमध्ये याचा वापर होतो. या पोस्टमध्ये आपण गुणोत्तर आणि प्रमाण यासंबंधी Shortcut Tricks, महत्त्वाच्या टिप्स आणि मूलभूत संकल्पना अगदी सोप्या भाषेत समजून घेणार आहोत.
गुणोत्तर आणि प्रमाण शॉर्टकट ट्रिक्स | Ratio and Proportion Shortcut Tricks in Marathi
गुणोत्तर म्हणजे काय? (What is Ratio?)
विशिष्ट परिस्थितीत दोन राशीची तुलना भागाकार पद्धतीने केल्यास ती गुणोत्तर म्हणतात. उदाहरणार्थ, 4:5 हे एक गुणोत्तर आहे, जे दर्शवते की पहिली संख्या दुसऱ्याच्या तुलनेत किती आहे.
गुणोत्तर लिहण्याची पद्धत:
- a/b
- a : b
- a ÷ b
पूर्वपद – a, उत्तरपद – b
प्रमाण म्हणजे काय? (What is Proportion?)
प्रमाण हे दोन गुणोत्तरांची समानता दर्शवणारे समीकरण आहे.
उदाहरण: 4/5 = 20/25 म्हणजेच 4:5 :: 20:25 हे प्रमाण आहे.
Must read : गुणोत्तर आणि प्रमाण – संपूर्ण माहिती
महत्त्वाचे Shortcut Tricks
Trick 1 – चतुर्थ प्रमाणपद काढा
जर प्रथम, द्वितीय, तृतीय आणि चतुर्थ प्रमाणपद अनुक्रमे a, b, c & d दिले असेल तर a×d=c×b किंवा a:b::c:d
- जर a : b :: c : d असेल, तर:
- प्रथम प्रमाणपद = a = bc/d
- द्वितीय प्रमाणपद = b = ad/c
- तृतीय प्रमाणपद = c = ad/b
- चतुर्थ प्रमाणपद = d = bc/a
उदाहरण 1 : 5, 20, 30 चे चतुर्थ प्रमाणपद काढा?
उत्तर :- चतुर्थ पद = ( 20× 30) / 5 = 120

Trick 2 – परंपरित प्रमाणात पदे काढणे
जर a, b & c या संख्या प्रमाणात असतील तर
- जर a, b, c परंपरित प्रमाणात असतील तर:
- प्रथमपद = a = (b²)/c
- मध्यमपद = b = √(ac)
- तृतीय पद = c = (b²)/a
उदाहरण 1 : 16 व 8 चे प्रथम प्रमाणपद काढा ?
उत्तर :- प्रथम प्रमाणपद=(16×16) /8=32
उदाहरण 2 : 49 & 81 चे मध्यम प्रमाणपद काढा?
उत्तर :- मध्यम प्रमाणपद = √(49 × 81) = 7 × 9 = 63
उदाहरण 3 : 4 & 6 चे तृतीय प्रमाणपद काढा?
उत्तर :- तृतीय प्रमाणपद = (6 × 6) /4 = 9

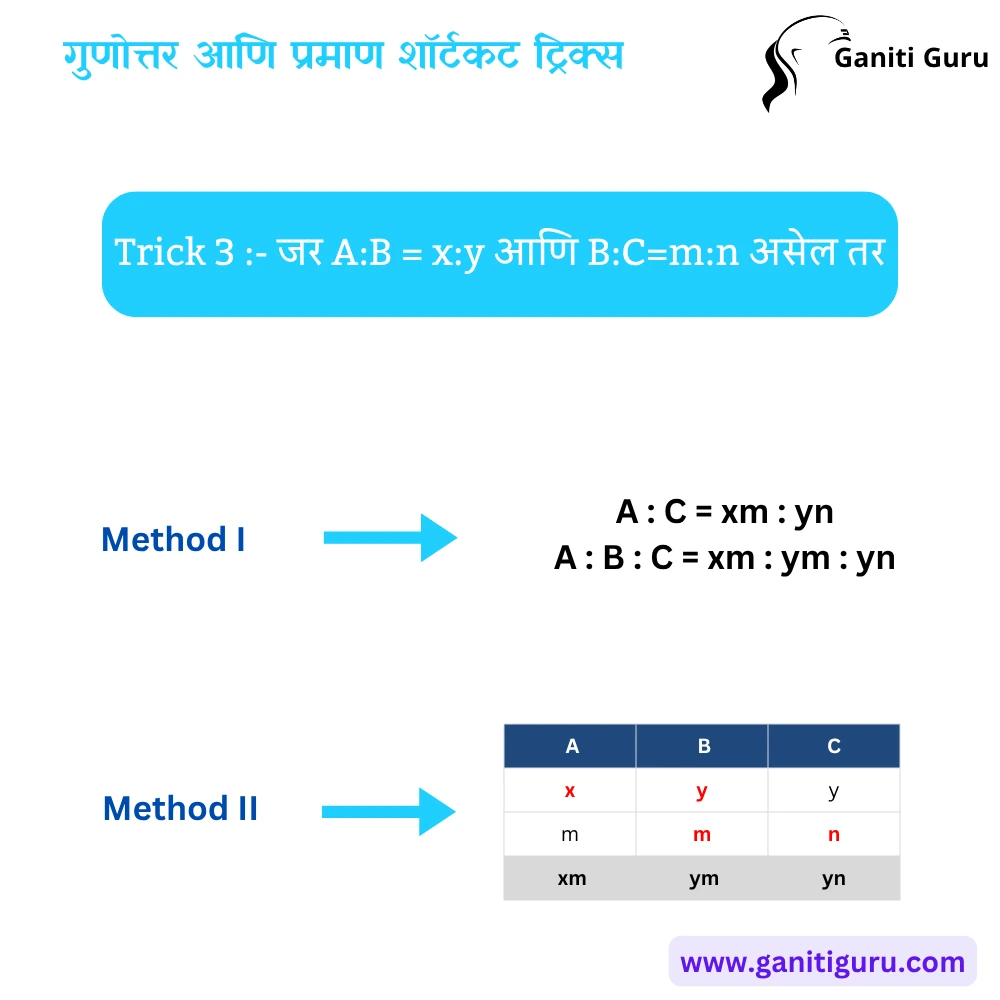
Trick 3 – मिश्र प्रमाण काढणे (A:B आणि B:C वरून A:B:C)
Method 1:
- जर A:B = x:y आणि B:C = m:n
- A:C = xm : yn
- A:B:C = xm : ym : yn
Method 2 – टेबल पद्धतीने :
| A | B | C |
|---|---|---|
| x | y | y |
| m | m | n |
| xm | ym | yn |
- उदाहरण 1:- A:B=7:9, B:C=3:5, A:B:C=?
- उत्तर :-
- A:B = 7:9, B:C = 3:5
- A:B:C = 21 : 27 : 45
| A | B | C |
|---|---|---|
| 7 | 9 | 9 |
| 3 | 3 | 5 |
| 21 | 27 | 45 |
- उदाहरण 2 : A:B=1:2, B:C=3:5, C:D=2:5, A:B:C:D=?
- उत्तर :- A:B:C:D = 6:12:20:50
| A | B | C | D |
| 1 | 2 | 2 | 2 |
| 3 | 3 | 5 | 5 |
| 2 | 2 | 2 | 5 |
| 6 | 12 | 20 | 50 |
Trick 4 – जर X राशीला A & B मध्ये a:b या गुणोत्तरा मध्ये विभागले असता
- A चा भाग = (a/(a+b)) × x
- B चा भाग = (b/(a+b)) × x
- A-B मधील अंतर = ((a−b)/(a+b)) × x
उदाहरण 1 : शनी आणि संभाजीनी मिळुन 6630 रुपये जमा केले जे की 4:9 च्या गुणोत्तरात आहे, तर शनीने किती रुपये जमा केले?
उत्तर :- शनी द्वारे जमा केलेली रक्कम = 4 × 6630 / 13 = 2040 रुपये
उदाहरण 2 : एका शाळेतील मुल आणि मुलीचे गुणोत्तर 8:5 आहे, जर शाळेत एकुण 416 जण असतील तर मुल आणि मुलीमधील अंतर किती?
उत्तर :- मुल आणि मुलीमधील अंतर = [(8 – 5) / (8 + 5)] × 416 = 96

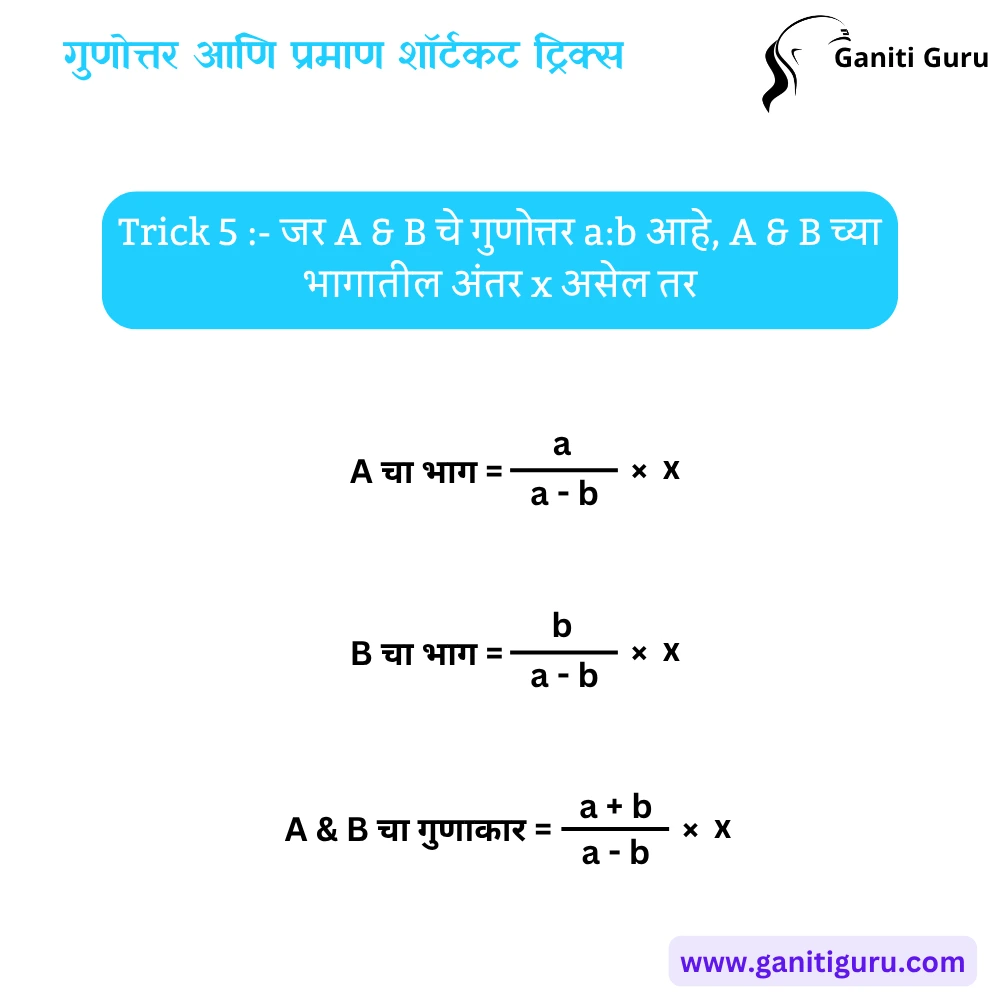
Trick 5 – जर A & B चे गुणोत्तर a:b आहे, A & B च्या भागातील अंतर x असेल तर
- A चा भाग = a/(a−b) × x
- B चा भाग = b/(a−b) × x
उदाहरण 1 : जर शनी आणि संभाजीला इंग्रजी विषयात मिळालेल्या गुणांचे गुणोत्तर 3:4 आहे आणि संभाजीला शनीपेक्षा 25 गुण जास्त मिळाले असेल तर शनीला इंग्रजी विषयात किती गुण मिळाले.
उत्तर :- शनीला मिळालेले गुण = 3 × 25 / (4 – 3 ) = 75
Trick 6 – जर A & B चे गुणोत्तर a:b आहे, आणि A चा भाग x असेल तर
- B चा भाग = (b/a) × A
- A-B मधील अंतर = (a−b)/a × A
- उदाहरण 1 : दोन संख्येचे गुणोत्तर 3:4 आहे, जर पहिली संख्या 81 असेल तर दुसरी संख्या किती?
- उत्तर :-
- दुसरी संख्या = 4 × 81 / 3 = 108
- दोन संख्यामधील अंतर = ( 4 – 3 ) × 81 / 3 = 27

Trick 7 – नाण्यांचे प्रमाण आणि एकूण रुपये
जर एका पिशवीमध्ये x रु., y रु. & z रु. च्या नोटाचे गुणोत्तर a:b:c आहे, जर पिशवीमध्ये R रुपये असले तर,
- x ची संख्या = a × R / (ax + by + cz)
- y ची संख्या = b × R / (ax + by + cz)
- z ची संख्या = c × R / (ax + by + cz)
- एकूण नोटा = ( a + b + c ) × R / (ax + by + cz)
- उदाहरण 1 : एका पिशवीमध्ये 25 पै., 19 पै. & 5 पै. च्या नोटाचे गुणोत्तर 1:2:3 आहे. जर पिशवीमध्ये एकुण 30 रु. असेल तर 5 पै. चे नाणी किती?
- उत्तर :- 5 पै. नाणी = 3 × 30 / ( 2.5 × 1 + 2 × 0.1 + 1.5 × 3 ) = 150

Trick 8 – जर A, B & C मध्ये एक राशी अनुक्रमे a:b:c या गुणोत्तरात वाटली असता, जर B ला x रु. मिळाले असेल तर
- A ला मिळालेले रु. =(ax)/b
- C ला मिळालेले रु. = (cx)/b
- उदाहरण 1 : जर A, B & C मध्ये एक राशी अनुक्रमे 2:3:2 च्या गुणोत्तरात वाटली असता जर A ला 600 रु. मिळत असेल तर B & C ला किती रु. मिळणार?
- उत्तर :-
- B = 600 × 3 / 2 = 900 रु.
- C = 600 × 1 / 2 = 300 रु.

Trick 9 – दोन वर्गांचे मुला-मुलीचे गुणोत्तर एकत्र करणे
- पहिल्या वर्गातील मुला-मूलीचे गुणोत्तर = a : b
- दुसऱ्या वर्गातील मुला-मूलीचे गुणोत्तर = c : d
- दोन्ही वर्गातील मुले एकत्र करून तिसऱ्या वर्गात बसवल्यावर तयार होणारे गुणोत्तर = a / ( a + b ) + c / ( c + d ) : b /( a + b ) + d / ( c + d )

Trick 10 – दुध-पाणी मिश्रणाचा अनुपात बदलण्यासाठी दुध किंवा पाणी किती वाढवावे हे शोधणे
- स्थिती 1 :
- a लिटर दूध आणि b लिटर पाणी यांच्या मिश्रणात किती दुध मिळवल्यावर c:d हे मिश्रण तयार होईल.
- मिळवावयाचे दूध = ( bc − ad ) / d
- उदाहरण 1 – दूध मिळवणे : एका भांड्यात 6 लिटर दूध आणि 2 लिटर पाणी आहे. त्यात दूध मिसळून दूध:पाणी = 5:1 करायचे आहे.
- a = 6, b = 2, c = 5, d = 1
- मिळवावयाचे दूध = ( 2 × 5 − 6 × 1 ) / 1 = 10 − 6 = 4 लिटर
- स्थिती 2 :
- a लिटर दूध आणि b लिटर पाणी यांच्या मिश्रणात किती पाणी मिळवल्यावर c:d हे मिश्रण तयार होईल.
- मिळवावयाचे पाणी = ( ad − bc ) / c
- उदाहरण 2 – पाणी मिळवणे :एका भांड्यात 9 लिटर दूध आणि 3 लिटर पाणी आहे. त्यात पाणी मिसळून दूध:पाणी = 3:2 करायचे आहे.
- a = 9, b = 3, c = 3, d = 2
- मिळवावयाचे पाणी = ( 9 × 2 − 3 × 3 ) / 3 = ( 18 − 9 ) / 3 = 3 लिटर

निष्कर्ष: Ratio and Proportion Shortcut Tricks in Marathi | Ganitiguru.com
गुणोत्तर आणि प्रमाण हा गणिताचा एक अत्यंत महत्त्वाचा आणि मूलभूत भाग आहे, जो शालेय अभ्यासक्रमात तसेच स्पर्धा परीक्षांमध्ये वारंवार विचारला जातो. या संकल्पनांचे नीटसे आकलन आणि स्मार्ट पद्धतीने सोडवण्याचे कौशल्य विकसित करणे अत्यावश्यक आहे.
या लेखात आपण पाहिले:
- गुणोत्तर म्हणजे दोन संख्यांची तुलनात्मक संख्या — जसे a : b
- प्रमाण म्हणजे दोन गुणोत्तरांमधील समानता — जसे a : b :: c : d
- महत्वाची सूत्रे व गुणधर्म — जसे ad = bc
- शॉर्टकट ट्रिक्स आणि सूत्रे – परीक्षेत जलद गणनेसाठी उपयुक्त
ganitiguru.com वर तुम्हाला गणिताच्या इतर विषयांसाठीही अशाच शॉर्टकट्स, सुलभ टिप्स आणि उदाहरणांसह मार्गदर्शन मिळेल.
गणितिगुरुला टेलीग्रामवर फॉलो करा


