सदिश आणि आदिश राशी | Scalar and Vector quantities in Marathi

विस्थापन (Displacement) :-

विस्थापन म्हणजे एखाद्या वस्तूच्या आरंभीच्या ठिकाणापासून अंतिम ठिकाणापर्यंत एका निश्चित दिशेत पार केलेले कमीत कमी अंतर.
हे अंतर व दिशा दोन्ही दर्शविते, त्यामुळे ते सदिश राशीच्या गटात मोडते.

• वैशिष्ट्ये:
  1. विस्थापन धन (Positive) असू शकते — जर अंतिम बिंदू प्रारंभ बिंदूपासून निवडलेल्या दिशेत असेल.
  2. विस्थापन ऋण (Negative) असू शकते — जर अंतिम बिंदू विरुद्ध दिशेत असेल.
  3. विस्थापन शून्य (Zero) असू शकते — जर वस्तू पुन्हा प्रारंभिक बिंदूवर आली.
• उदाहरण:
  समजा, एक माणूस 4 मीटर पूर्व दिशेला चालला आणि नंतर 4 मीटर पश्चिम दिशेला परत आला. त्याने एकूण 8 मीटर अंतर कापले असले तरी विस्थापन शून्य आहे, कारण अंतिम बिंदू प्रारंभ बिंदूशी जुळतो.

वेग (Velocity)

व्याख्या:
एखाद्या वस्तूच्या विस्थापनाचा दर म्हणजेच त्या वस्तूचा वेग (Velocity) होय.
म्हणजेच, निश्चित दिशेत वेळेनुसार विस्थापन किती जलद बदलते हे वेग दर्शवतो.

सूत्र: v=Δs/Δt

इथे,

• v = वेग
• Δs = विस्थापन
• Δt = घेतलेला वेळ

वैशिष्ट्ये:

1. वेग ही सदिश राशी आहे — याला परिमाण (Magnitude) व दिशा (Direction) दोन्ही असतात.
2. वेग धन, ऋण किंवा शून्य असू शकतो.
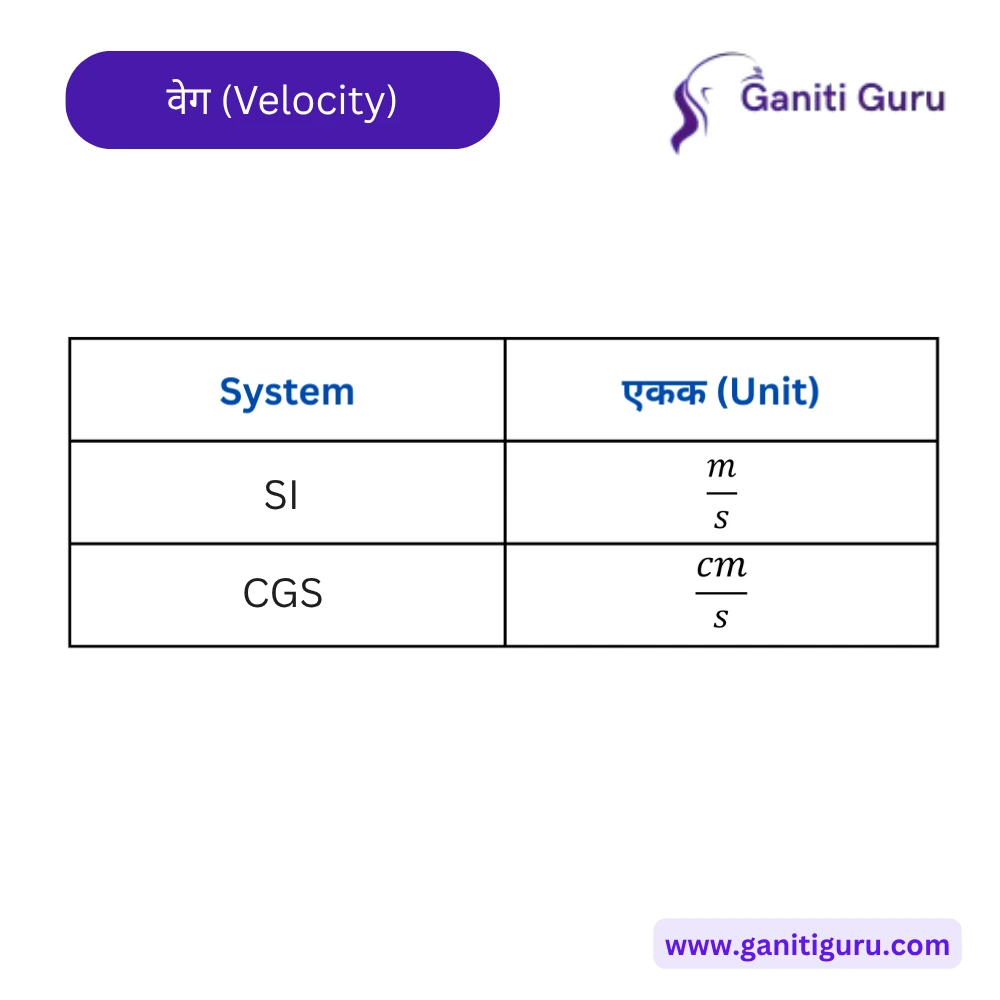
3. वेगाच्या मापनासाठी SI एकक — मीटर प्रति सेकंद (m/s).

उदाहरण:
जर एक कार 100 मीटर अंतर 20 सेकंदात पूर्व दिशेला सरकत असेल, तर v=100/20=5 m/s पूर्व

येथे “5 m/s पूर्व” हा वेग आहे.

त्वरण (Acceleration)

व्याख्या:
एकक काळात (Unit time) वेगात झालेला बदल म्हणजे त्वरण (Acceleration) होय.
म्हणजेच, वेग वेळेनुसार किती जलद वाढतो किंवा कमी होतो हे त्वरण दर्शवते.

सूत्र: a=(v−u)t

इथे,

• a = त्वरण (Acceleration)
• v = अंतिम वेग (Final velocity)
• u = प्रारंभिक वेग (Initial velocity)
• t = घेतलेला वेळ (Time)

वैशिष्ट्ये:

1. त्वरण ही सदिश राशी आहे — याला परिमाण आणि दिशा दोन्ही असतात.
2. त्वरण धन (Positive) असल्यास वस्तूचा वेग वाढतो.
3. त्वरण ऋण (Negative) असल्यास वस्तूचा वेग कमी होतो, याला मंदन (Retardation) किंवा ऋण त्वरण म्हणतात.
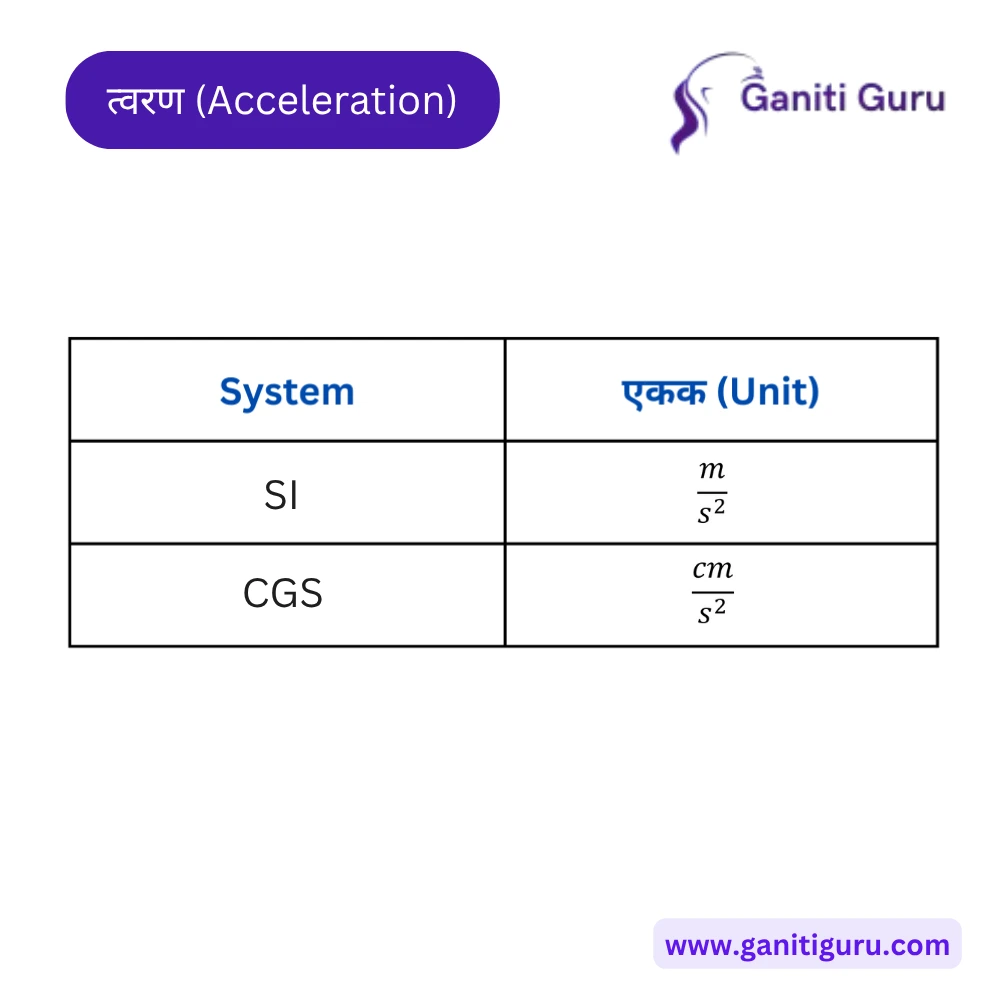
4. SI एकक — मीटर प्रति सेकंद² (m/s²).

उदाहरण:
एखादी सायकल सुरुवातीला स्थिर (0 m/s) आहे आणि 5 सेकंदांत तिचा वेग 10 m/s होतो. a = (10−0)/5 = 2 m/s²

म्हणजे सायकलचा त्वरण 2 m/s² आहे.

बल (Force)

व्याख्या:
अचल वस्तूला गतीमान करण्यासाठी, गतीमान वस्तूची गती थांबवण्यासाठी किंवा सरळ रेषेत एकसमान गतीत बदल करण्यासाठी आवश्यक असणारी भौतिक रक्कम म्हणजे बल (Force) होय.
म्हणजेच, बलामुळे वस्तूच्या वेगात किंवा दिशेत बदल होतो किंवा वस्तू विकृत (Shape बदलणे) होऊ शकते.

सूत्र (न्यूटनचा दुसरा नियम): F=m×a

इथे,

• F = बल (Force)
• m = वस्तूचे वस्तुमान (Mass)
• a = त्वरण (Acceleration)

वैशिष्ट्ये:

1. बल ही सदिश राशी आहे — याला परिमाण आणि दिशा असते.
2. बलामुळे वस्तूचा वेग वाढू किंवा कमी होऊ शकतो.
3. बलामुळे वस्तूची दिशा बदलू शकते.
4. बलामुळे वस्तूचा आकार आणि आकारमान बदलू शकतो.
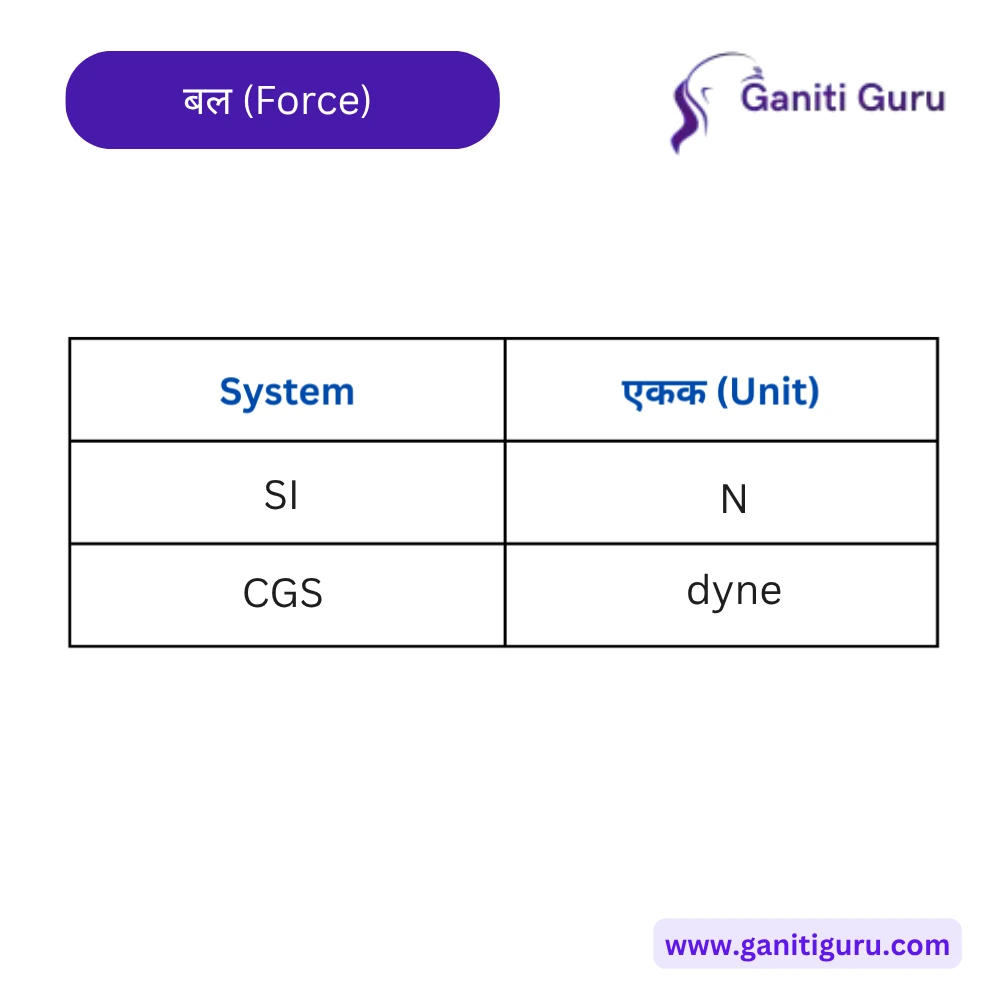
5. SI एकक — न्यूटन (Newton).

उदाहरण:
जर 2 kg वस्तूवर 3 m/s² त्वरण निर्माण करायचे असेल, F=2×3=6 N

म्हणजे त्या वस्तूवर 6 न्यूटन बल लावावे लागेल.

वजन (Weight)

व्याख्या:
एखाद्या वस्तूवर पृथ्वी ज्या गुरुत्वीय बलाने आकर्षण करते त्या बलाला वस्तूचे वजन (Weight) म्हणतात.
याची दिशा नेहमी पृथ्वीच्या केंद्राकडे असते.

वैशिष्ट्ये:

1. सदिश राशी आहे — परिमाण आणि दिशा असते.
2. वस्तूचे वजन हे स्थानावर अवलंबून बदलते कारण गुरुत्व त्वरण (ggg) वेगवेगळ्या ठिकाणी वेगळे असते.
3. पृथ्वीच्या केंद्राशी वस्तूचे वजन शून्य असते.
4. चंद्रावर किंवा इतर ग्रहांवर वजन वेगळे असते.

सूत्र: W=m×g

इथे,

• W = वजन (Weight)
• m = वस्तूचे वस्तुमान (Mass)
• g = गुरुत्वाकर्षणामुळे होणारे त्वरण (9.8 m/s² पृथ्वीवर)

उदाहरण:
जर वस्तूचे वस्तुमान m=10 kg असेल, W=10×9.8=98 N

म्हणजे त्या वस्तूचे वजन पृथ्वीवर 98 न्यूटन आहे.

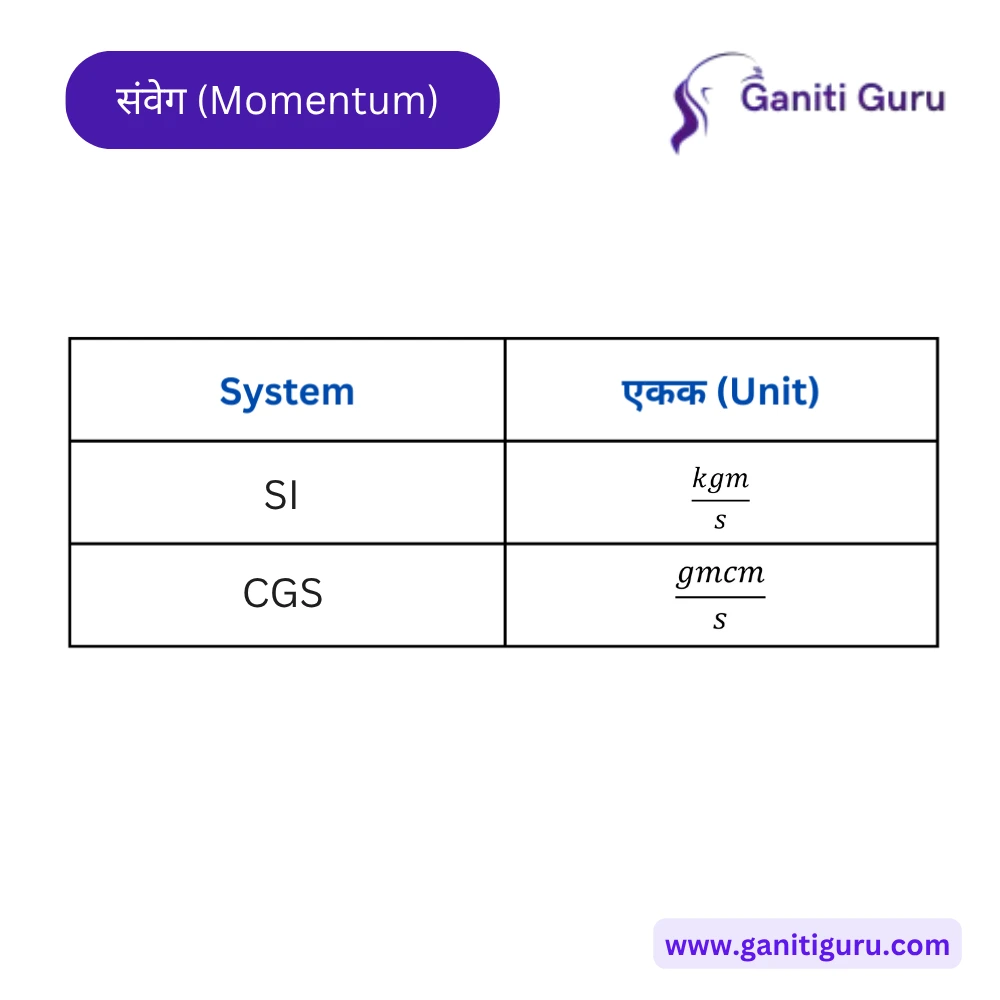
संवेग (Momentum)

व्याख्या:
एखाद्या वस्तूच्या वस्तूमान (Mass) आणि तिच्या वेग (Velocity) यांच्या गुणाकाराला संवेग (Momentum) म्हणतात.
संवेग हा वस्तूच्या गतीचे परिमाण दर्शवतो.

सूत्र: P=m×v

इथे,

• P = संवेग (Momentum)
• m = वस्तूमान (Mass)
• v = वेग (Velocity)

वैशिष्ट्ये:

1. संवेग ही सदिश राशी आहे, कारण त्याला परिमाणाबरोबर दिशा देखील असते.
2. वस्तूचा वेग जास्त किंवा वस्तूमान जास्त असेल, तर संवेग देखील जास्त असतो.
3. संवेगाची दिशा नेहमी वस्तूच्या वेगाच्या दिशेसारखी असते.

एकक:
SI पद्धतीत संवेगाचे एकक आहे — किलोग्रॅम·मीटर/सेकंद (kg·m/s)

उदाहरण:
जर वस्तूचे वस्तूमान 5 kg आणि वेग 3 m/s असेल, P=5×3=15 kg·m/s

म्हणजे त्या वस्तूचा संवेग 15 kg·m/s आहे.

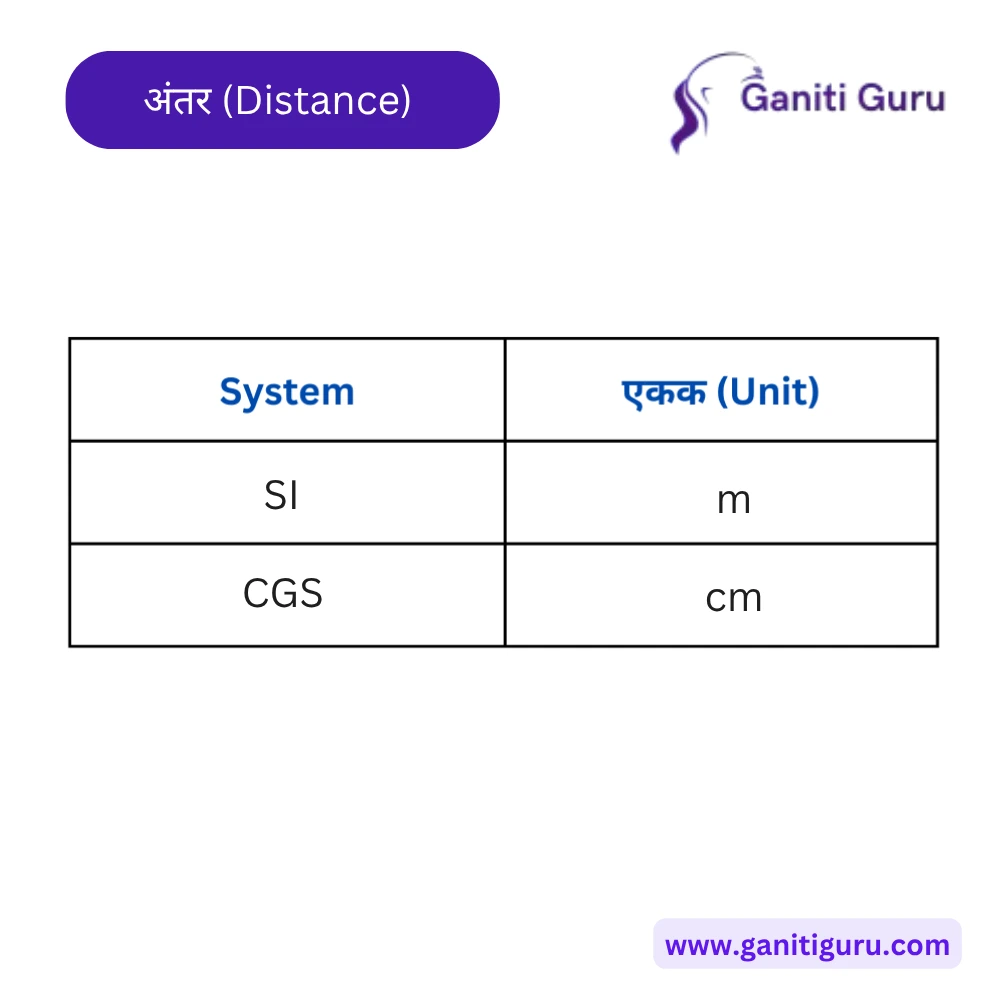
अंतर (Distance):

व्याख्या:
एखाद्या गतिमान वस्तूने दिशेचा विचार न करता प्रत्यक्ष पार केलेल्या मार्गाची लांबी म्हणजे अंतर (Distance) होय.

वैशिष्ट्ये:

• अंतर हे अदिश राशी आहे.
• अंतराचे मूल्य नेहमी धन (Positive) असते, शून्य किंवा ऋण होत नाही.
• मोजणीसाठी मार्गाची लांबी घेतली जाते, सुरुवातीचे व शेवटचे स्थान यामधील दिशा महत्त्वाची नसते.
• एकक: मीटर (m) — आंतरराष्ट्रीय एकक प्रणाली (SI).

उदाहरण:
जर एखादा माणूस 5 मीटर पुढे आणि मग 3 मीटर मागे चालला, तर एकूण अंतर = 5 + 3 = 8 मीटर, जरी त्याचे विस्थापन 2 मीटर असेल.

लांबी (Length):

व्याख्या:
कोणत्याही दोन बिंदूमधील अंतरास लांबी (Length) म्हणतात.

वैशिष्ट्ये:

• लांबी ही अदिश राशी आहे.
• तिचे मोजमाप दिशेशी संबंध नसतो — फक्त परिमाण महत्त्वाचे असते.
• एकक (SI): मीटर (m).
• लांबी ही अंतर मोजण्याचे मूलभूत माप आहे आणि इतर अनेक भौतिक राशींच्या परिभाषेत वापरली जाते.

उदाहरणे:

• टेबलची लांबी = 1.5 मीटर
• रस्त्याच्या दोन टोकांमधील लांबी = 2 किलोमीटर

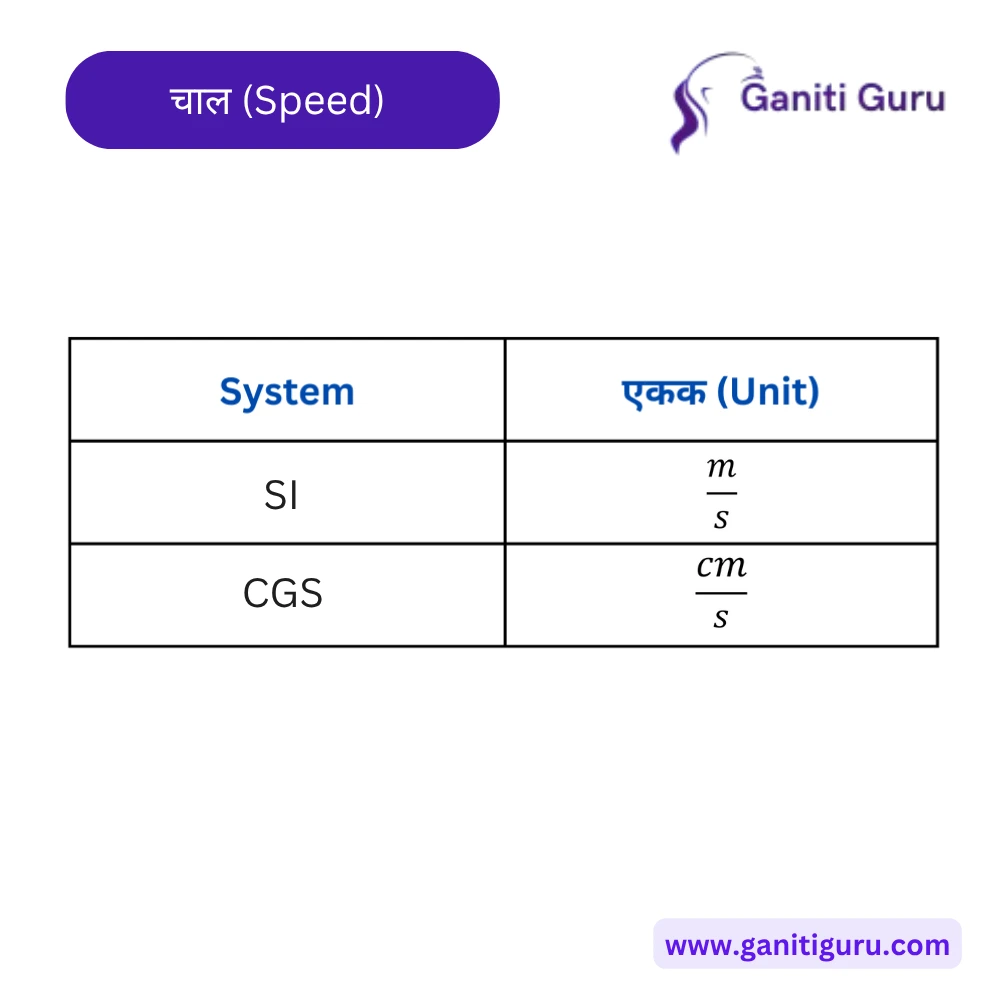
चाल (Speed):

व्याख्या:
एकक कालावधीमध्ये वस्तूने आक्रमिलेले (कापलेले) अंतर म्हणजेच त्या वस्तूची चाल (Speed) होय.

सूत्र: चाल=अंतर/काळ

वैशिष्ट्ये:

• चाल ही अदिश राशी आहे.
• गतीची दिशा विचारात घेतली जात नाही.
• SI एकक: मीटर प्रति सेकंद (m/s).
• चाल सदैव धन मूल्याची असते.

उदाहरणे:

• कारने 2 तासांत 100 किमी अंतर पार केले → चाल = 100/2=50 किमी/तास
• धावपटूने 10 सेकंदांत 100 मीटर धावले → चाल = 100/10=10 मी/से

वस्तुमान (Mass):

व्याख्या:
पदार्थातील द्रव्यसंचयाला म्हणजेच किती प्रमाणात द्रव्य आहे, याला वस्तुमान (Mass) म्हणतात.

वैशिष्ट्ये:

• वस्तुमान हे जडत्वाचे गुणात्मक माप आहे.
• जडत्व म्हणजे पदार्थाच्या नैसर्गिक स्थितीबदलास विरोध करण्याची प्रवृत्ती.
• जितके वस्तुमान जास्त, तितके जडत्व जास्त असते.
• वस्तुमान स्थळानुसार बदलत नाही, म्हणजेच पृथ्वीवर, चंद्रावर किंवा अवकाशात वस्तुमान समान राहते.

SI एकक: किलोग्रॅम (kg)
CGS एकक: ग्रॅम (g)

उदाहरणे:

• पाण्याच्या बाटलीचे वस्तुमान 1.5 kg
• क्रिकेट चेंडूचे वस्तुमान 156 g

वेळ (Time):

व्याख्या:
घटनांच्या घडामोडींचा कालक्रम मोजण्यासाठी वापरली जाणारी भौतिक रक्कम म्हणजे वेळ (Time).

मानक परिभाषा:

• एक सौर दिन = पृथ्वीने स्वतःभोवती एक फेरी पूर्ण करण्यास लागणारा सरासरी वेळ.
• 1 सेकंद = 1 सौर दिनाचा 1/86400 वा भाग.

एकके:

• 1 मिनिट = 60 सेकंद
• 1 तास = 60 मिनिटे = 3600 सेकंद

SI एकक: सेकंद (s)

उदाहरणे:

• सूर्य उगवण्यापासून मावळण्यापर्यंतचा वेळ ≈ 12 तास
• 100 मीटर धावण्याचा वेळ ≈ 10 सेकंद

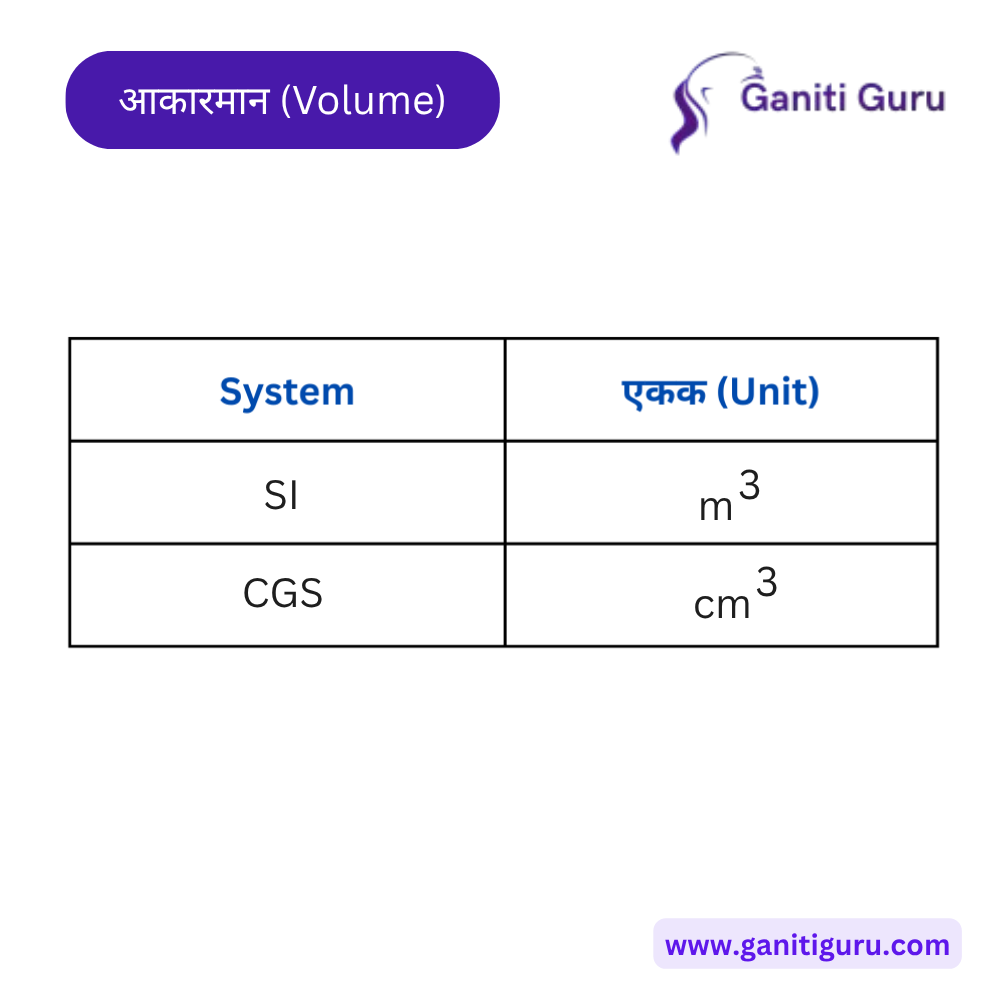
आकारमान (Volume):

व्याख्या:
एखाद्या पदार्थाने व्यापलेली त्रिमितीय (3D) जागा म्हणजे आकारमान (Volume) होय.

एकके:

• SI एकक: घन मीटर (m³)
• इतर प्रचलित एकके: लिटर (L), मिलिलिटर (mL), घन सेंटीमीटर (cm³)

सूत्रे:

• घन (Cube): V=a³ (इथे a = बाजूची लांबी)
• आयतघन (Cuboid): V=l×b×h

उदाहरण:

• पाण्याच्या बाटलीचे आकारमान = 1 लिटर = 1000 cm³

घनता (Density):

व्याख्या:
एखाद्या पदार्थाच्या एकक आकारमानात (unit volume) असलेल्या वस्तुमानाला त्या पदार्थाची घनता (Density) म्हणतात.

सूत्र: घनता(ρ)=वस्तुमान (m)आकारमान (V)\text{घनता} (\rho) = \frac{\text{वस्तुमान (m)}}{\text{आकारमान (V)}}घनता(ρ)=आकारमान (V)वस्तुमान (m)​

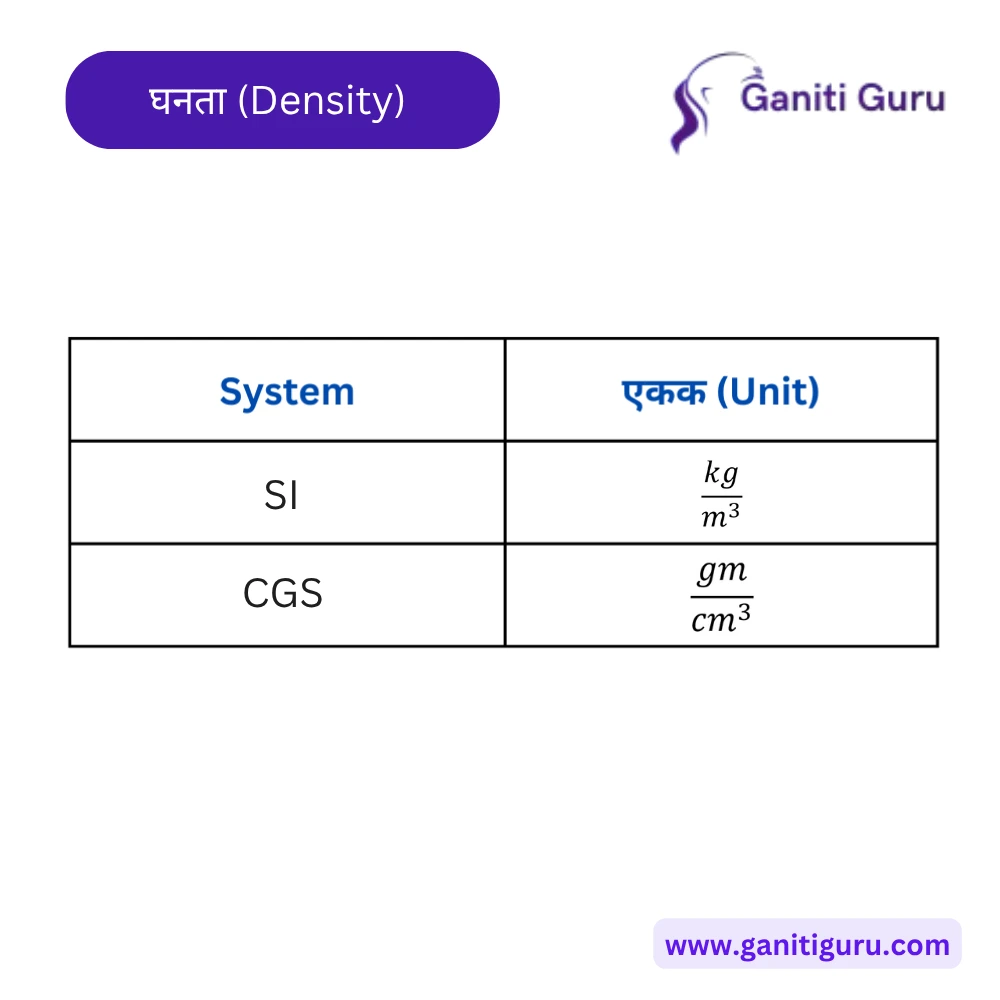
SI एकक:

• किलोग्राम प्रति घन मीटर (kg/m³)
• इतर प्रचलित एकके: ग्राम प्रति घन सेंटीमीटर (g/cm³)

उदाहरण:

• पाण्याची घनता = 1000 kg/m³ किंवा 1 g/cm³