3 चा पाढा | Table of 3 in Marathi

3 चा पाढा | Table of 3 in Marathi

गणित शिकताना पाढे हा पाया मानला जातो. २ चा पाढा शिकून झाल्यानंतर पुढील टप्पा म्हणजे ३ चा पाढा. हा पाढा विद्यार्थ्यांना गुणाकाराची सवय लावतो आणि त्यांची गणनेची गती वाढवतो. ३ चा पाढा शिकल्यानंतर वेळ, प्रमाण, मोजमाप, पैशांची बेरीज-वजाबाकी अशा दैनंदिन जीवनातील अनेक गोष्टी सोप्या होतात.

३ चा पाढा हा विषम व सम संख्यांचा आलटून-पालटून येणारा क्रम असल्याने तो लक्षात ठेवणे सोपे जाते. योग्य उच्चार, लिखाण आणि नियमित सरावाने हा पाढा पटकन लक्षात राहतो आणि पुढील कठीण पाढे शिकणे सोपे होते.

3 चा पाढा म्हणजे काय?

3 चा पाढा म्हणजे 3 या संख्येच्या पुनरावृत्तीने होणारा गुणाकार. म्हणजेच, एखाद्या संख्येला 3 ने गुणिले म्हणजे त्या संख्येइतक्या वेळा 3 ची बेरीज केली जाते.

उदा.:

• 3 × 1 = 3
• 3 × 3 = 3 + 3 = 6
• 3 × 3 = 3 + 3 + 3 = 9

याप्रमाणे 3, 6, 9, 12, 15, 18, 21, 24, 27, 30… हा क्रम तयार होतो.

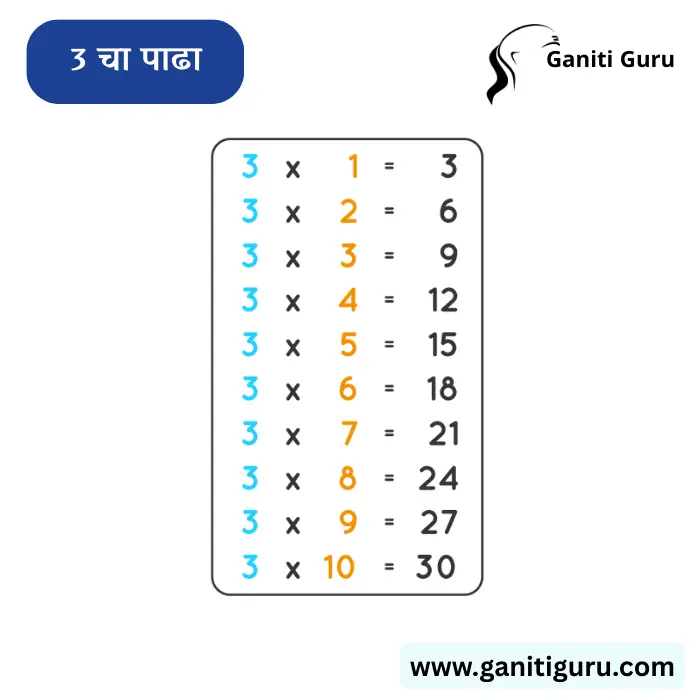
3 चा पाढा (1 ते 20 पर्यंत) | Multiplication Table of 3 in Marathi

3	x	1	=	3
3	x	2	=	6
3	x	3	=	9
3	x	4	=	12
3	x	5	=	15
3	x	6	=	18
3	x	7	=	21
3	x	8	=	24
3	x	9	=	27
3	x	10	=	30
3	x	11	=	33
3	x	12	=	36
3	x	13	=	39
3	x	14	=	42
3	x	15	=	45
3	x	16	=	48
3	x	17	=	51
3	x	18	=	54
3	x	19	=	57
3	x	20	=	60

3 चा पाढा वाचण्याची पद्धत (मराठीत)

तीन एके तीन
तीन दुने सहा
तीन तिके नऊ
तीन चौक बारा
तीन पांचे पंधरा
तीन सहा अठरा
तीन साते एकवीस
तीन आठे चोवीस
तीन नव्वे सत्तावीस
तीन दहावे तीस

How to Read 3 Times Table in English

Three ones are three
Three twos are six
Three threes are nine
Three fours are twelve
Three fives are fifteen
Three sixes are eighteen
Three sevens are twenty-one
Three eights are twenty-four
Three nines are twenty-seven
Three tens are thirty

सोडवलेली उदाहरणे

निष्कर्ष

3 चा पाढा हा गणितातील एक महत्त्वाचा पायरी आहे. याचा नियमित सराव केल्यास केवळ गुणाकारच नव्हे, तर इतर गणिती क्रिया देखील सोप्या आणि जलद होतील.

GanitiGuru कडून आणखी अशा रंजक व सोप्या गणिती ट्रिक्स जाणून घेण्यासाठी आमचे पेज फॉलो करा!

गणितिगुरुला टेलीग्रामवर फॉलो करा